Python math function | hypot()

hypot() function is an inbuilt math function in Python that return the Euclidean norm, 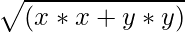. Syntax :

hypot(x, y) 

Parameters :

x and y are numerical values 

Returns :

Returns a float value having Euclidean norm, sqrt(x*x + y*y). 

Error :

When more than two arguments are 
passed, it returns a TypeError.

Note : One has to import math module before using hypot() function.   Below is the demonstration of hypot() function : Code #1 : 

Python3

# Python3 program for hypot() function

# Import the math module
import math

# Use of hypot function
print("hypot(3, 4) : ", math.hypot(3, 4))

# Neglects the negative sign
print("hypot(-3, 4) : ", math.hypot(-3, 4))

print("hypot(6, 6) : ", math.hypot(6, 6))

Output :

hypot(3, 4) :  5.0
hypot(-3, 4) :  5.0
hypot(6, 6) :  8.48528137423857

Code #2 : 

Python3

# Python3 program for error in hypot() function

# import the math module
import math

# Use of hypot() function
print("hypot(3, 4, 6) : ",  math.hypot(3, 4, 6))

Output : 

Traceback (most recent call last):
  File "/home/d8c8612ee97dd2c763e2836de644fac1.py", line 7, in 
    print("hypot(3, 4, 6) : ",  math.hypot(3, 4, 6))
TypeError: hypot expected 2 arguments, got 3

Practical Application : Given perpendicular and base of a right angle triangle find the hypotenuse. Using Pythagorean theorem which states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Hence,

 Hypotenuse = sqrt(p^2 + b^2) 

Code #3 :

Python3

# Python3 program for finding Hypotenuse
# in hypot() function

# import the math module
from math import hypot

# Perpendicular and base
p = 3
b = 4

# Calculates the hypotenuse
print("Hypotenuse is:", hypot(p, b))

Output :

Hypotenuse is: 5.0