Python | How and where to apply Feature Scaling?
Last Updated :
23 Dec, 2022
Feature Scaling or Standardization: It is a step of Data Pre Processing that is applied to independent variables or features of data. It helps to normalize the data within a particular range. Sometimes, it also helps in speeding up the calculations in an algorithm.
Package Used:
sklearn.preprocessing
Import:
from sklearn.preprocessing import StandardScaler
The formula used in the Backend
Standardization replaces the values with their Z scores.
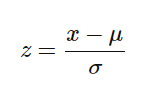
Mostly the Fit method is used for Feature scaling
fit(X, y = None)
Computes the mean and std to be used for later scaling.
Python
import pandas as pd
from sklearn.preprocessing import StandardScaler
data = read_csv('Geeksforgeeks.csv')
data.head()
scaler = StandardScaler()
scaler.fit(data)
|
Why and Where to Apply Feature Scaling?
The real-world dataset contains features that highly vary in magnitudes, units, and range. Normalization should be performed when the scale of a feature is irrelevant or misleading and should not normalize when the scale is meaningful.
The algorithms which use Euclidean Distance measures are sensitive to Magnitudes. Here feature scaling helps to weigh all the features equally.
Formally, If a feature in the dataset is big in scale compared to others then in algorithms where Euclidean distance is measured this big scaled feature becomes dominating and needs to be normalized.

feature scaling in python ( image source- by Jatin Sharma )
Examples of Algorithms where Feature Scaling matters
1. K-Means uses the Euclidean distance measure here feature scaling matters.
2. K-Nearest-Neighbors also require feature scaling.
3. Principal Component Analysis (PCA): Tries to get the feature with maximum variance, here too feature scaling is required.
4. Gradient Descent: Calculation speed increase as Theta calculation becomes faster after feature scaling.
Note: Naive Bayes, Linear Discriminant Analysis, and Tree-Based models are not affected by feature scaling.
In Short, any Algorithm which is Not Distance-based is Not affected by Feature Scaling.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...