Python – Find the maximum number of triangles with given points on three lines

Given three parallel straight lines l1, l2 and l3 lying in the same plane. Total numbers of m, n and k points lie on the line l1, l2, l3 respectively. This article aims to find the maximum number of triangles formed with vertices at these points. 

Examples:

Input : m = 14, n = 34, k = 114 
Output : 448708.0

Input : m = 95, n = 77, k = 94 
Output : 2755951.0 

Approach:

1. Total number of triangle = 
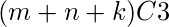
2. Number of triangles that is not valid triangle from l1 plane = 
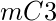
3. Number of triangles that is not valid triangle from l2 plane = 
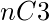
4. Number of triangles that is not valid triangle from l3 plane = 
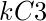
5. so number of valid Triangle = 

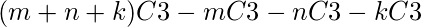
Below is the Python code implementation of the approach.

Python3

# Python code implementation
import math
def nooftriangle(m, n, k):

    # r1 = (m + n + k)C3
    r1 = math.factorial(m + n + k) / (
            math.factorial(3) * math.factorial(m + n + k - 3))
    # r2 = mC3
    r2 = math.factorial(m) / (math.factorial(3) * math.factorial(m - 3))

    # r3 = nC3
    r3 = math.factorial(n) / (math.factorial(3) * math.factorial(n - 3))

    #r4 = kC3
    r4 = math.factorial(k) / (math.factorial(3) * math.factorial(k - 3))

    result = r1 - r2 - r3 - r4
    return(result)

# Driver code
m = 17
n = 16
k = 11
print("Number of triangles : ", nooftriangle(m, n, k))

Output:

Number of triangles :  11839.0

Time Complexity: O(m+n+k)

Auxiliary Space: O(1)