Python | Fast Walsh Hadamard Transform

Fast Walsh Hadamard Transform, is an Hadamard ordered efficient algorithm to compute the Walsh Hadamard transform (WHT). Normal WHT computation has N = 2^m complexity but using FWHT reduces the computation to O(n²). The FWHT requires O(n logn) additions and subtraction operations. It is a divide and conquer algorithm which breaks down the WHT recursively. 

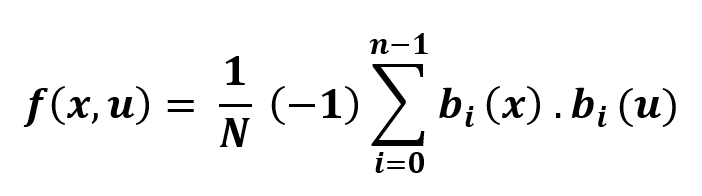
sympy.discrete.transforms.fwht( ) : It can perform Walsh Hadamard Transform (WHT). This method uses Hadamard sequence ordering. 
Automatically the sequence is padded with zero to the right because the radix-2 FWHT requires the sample point number as a power of 2. 

Parameters : 
-> seq : [iterable] sequence on which WHT is to be applied.

Returns : 
Fast Walsh Hadamard Transform Transform

Example #1 : 

Python3

# import sympy
from sympy import fwht

# sequence
seq = [23,
       56,
       12,
       555]

# hwht
transform = fwht(seq)
print ("Transform  : ", transform)

Output : 

Transform  :  [646, -576, -488, 510]

Example #2 : 

Python3

# import sympy
from sympy import fwht

# sequence
seq = [15, 21, 13, 44]

# hwht
transform = fwht(seq)
print ("Transform  : ", transform)

Output : 

Transform  :  [93, -37, -21, 25]