Pythagorean Triplet with given sum using single loop
Last Updated :
06 Apr, 2023
A Pythagorean Triplet is a set of natural numbers such that a < b < c, for which
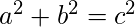
Given a number N, find a Pythagorean Triplet with sum as given N or return -1.
Examples:
Input: 12
Output: 3 4 5
Explanation:
As 32 + 42 = 52
Input: 82
Output: -1
Approach: The idea is to find the value of b and c in terms of a and iterate a from 1 to N. To find the value of b and c in terms of a we have to do following:
We have two equations,
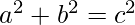

We will find the value of c in term of a and b Then put this value in equation 1 to solve for b.
From equation 2,

Now, put this value in equation 1.
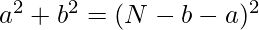
After solving the above equation we will get,
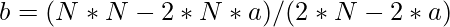

Now, iterate a from 1 to N and calculate respectively the value of b and c Then, check if
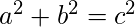
C++
#include <bits/stdc++.h>
using namespace std;
void PythagoreanTriplet(int n)
{
int flag = 0;
for (int a = 1; a < n; a++)
{
int b = (n * n - 2 * n * a)
/ (2 * n - 2 * a);
int c = n - a - b;
if (a * a + b * b == c * c
&& b > 0 && c > 0)
{
cout << a << " " << b << " " << c;
flag = 1;
break;
}
}
if (flag == 0) {
cout << "-1";
}
return;
}
int main()
{
int N = 12;
PythagoreanTriplet(N);
return 0;
}
|
Java
class GFG {
static void PythagoreanTriplet(int n)
{
int flag = 0;
for (int a = 1; a < n; a++)
{
int b = (n * n - 2 * n * a)
/ (2 * n - 2 * a);
int c = n - a - b;
if (a * a + b * b == c * c
&& b > 0 && c > 0)
{
System.out
.print(a + " " + b + " " + c);
flag = 1;
break;
}
}
if (flag == 0)
{
System.out.print("-1");
}
return;
}
public static void main(String[] args)
{
int N = 12;
PythagoreanTriplet(N);
}
}
|
Python3
def PythagoreanTriplet(n):
flag = 0
for a in range(1, n, 1):
b = (n * n - 2 * n * a) // (2 * n - 2 * a)
c = n - a - b
if (a * a + b * b == c * c
and b > 0 and c > 0):
print(a, b, c)
flag = 1
break
if(flag == 0):
print("-1")
return
if __name__ == '__main__':
N = 12
PythagoreanTriplet(N)
|
C#
using System;
class GFG {
static void PythagoreanTriplet(int n)
{
int flag = 0;
for (int a = 1; a < n; a++)
{
int b = (n * n - 2 * n * a)
/ (2 * n - 2 * a);
int c = n - a - b;
if (a * a + b * b == c * c
&& b > 0 && c > 0)
{
Console.Write(a + " " + b + " " + c);
flag = 1;
break;
}
}
if (flag == 0) {
Console.Write("-1");
}
return;
}
public static void Main(String[] args)
{
int N = 12;
PythagoreanTriplet(N);
}
}
|
Javascript
<script>
function PythagoreanTriplet(n)
{
let flag = 0;
for (let a = 1; a < n; a++)
{
let b = (n * n - 2 * n * a)
/ (2 * n - 2 * a);
let c = n - a - b;
if (a * a + b * b == c * c
&& b > 0 && c > 0)
{
document.write(a + " " + b + " " + c);
flag = 1;
break;
}
}
if (flag == 0) {
document.write("-1");
}
return;
}
let N = 12;
PythagoreanTriplet(N);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...