Pythagorean Quadruple

Given four points, check whether they form Pythagorean Quadruple. 
It is defined as a tuple of integers a, b, c, d such that 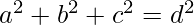. They are basically the solutions of Diophantine Equations. In the geometric interpretation it represents a cuboid with integer side lengths |a|, |b|, |c| and whose space diagonal is |d| . 

The cuboids sides shown here are examples of pythagorean quadruples. 
It is primitive when their greatest common divisor is 1. Every Pythagorean quadruple is an integer multiple of a primitive quadruple. We can generate the set of primitive pythagorean quadruples for which a is odd can be generated by formula :

a = m² + n² – p² – q², 
b = 2(mq + np), 
c = 2(nq – mp), 
d = m² + n² + p² + q²

where m, n, p, q are non-negative integers with greatest common divisor 1 such that m + n + p + q are odd. Thus, all primitive Pythagorean quadruples are characterized by Lebesgue’s identity.

(m² + n² + p² + q²)² = (2mq + 2nq)² + 2(nq – mp)² + (m² + n² – p² – q²)m² + n² – p² – q²

C++

// C++ code to detect Pythagorean Quadruples.
#include <bits/stdc++.h>
using namespace std;

// function for checking
bool pythagorean_quadruple(int a, int b, int c,
                                        int d)
{
    int sum = a * a + b * b + c * c;
    if (d * d == sum)
        return true;
    else
        return false;
}

// Driver Code
int main()
{
    int a = 1, b = 2, c = 2, d = 3;
    if (pythagorean_quadruple(a, b, c, d))
        cout << "Yes" << endl;
    else
        cout << "No" << endl;
}

Java

// Java code to detect Pythagorean Quadruples.
import java.io.*;
import java.util.*;

class GFG {

// function for checking
static Boolean pythagorean_quadruple(int a, int b,
                                   int c, int d)
{
    int sum = a * a + b * b + c * c;
    if (d * d == sum)
        return true;
    else
        return false;
}

// Driver function
    public static void main (String[] args) {
    int a = 1, b = 2, c = 2, d = 3;
    if (pythagorean_quadruple(a, b, c, d))
        System.out.println("Yes");
    else
        System.out.println("No" );

    }
}
// This code is contributed by Gitanjali.

Python3

# Python  code to detect
# Pythagorean Quadruples.
import math

# function for checking
def pythagorean_quadruple(a,b, c, d):

    sum = a * a + b * b + c * c;
    if (d * d == sum):
        return True
    else:
        return False

#driver code
a = 1
b = 2
c = 2
d = 3
if (pythagorean_quadruple(a, b, c, d)):
    print("Yes")
else:
     print("No" )

# This code is contributed
# by Gitanjali.

C#

// C# code to detect
// Pythagorean Quadruples.
using System;

class GFG {

    // function for checking
    static Boolean pythagorean_quadruple(int a,
                            int b, int c, int d)
    {
        int sum = a * a + b * b + c * c;
        if (d * d == sum)
            return true;
        else
            return false;
    }

    // Driver function
        public static void Main () {

        int a = 1, b = 2, c = 2, d = 3;

        if (pythagorean_quadruple(a, b, c, d))
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No" );

    }
}

// This code is contributed by vt_M.

PHP

<?php
// php code to detect Pythagorean Quadruples.

// function for checking
function pythagorean_quadruple($a, $b, $c, $d)
{
    $sum = $a * $a + $b * $b + $c * $c;

    if ($d * $d == $sum)
        return true;
    else
        return false;
}

// Driver Code
    $a = 1; $b = 2; $c = 2; $d = 3;

    if (pythagorean_quadruple($a, $b, $c, $d))
        echo "Yes" ;
    else
        echo "No" ;

// This code is contributed by anuj_67.
?>

Javascript

<script>

// JavaScript program to detect Pythagorean Quadruples.

// function for checking
function pythagorean_quadruple(a, b,
                                   c, d)
{
    let sum = a * a + b * b + c * c;
    if (d * d == sum)
        return true;
    else
        return false;
}


// Driver code

        let a = 1, b = 2, c = 2, d = 3;
    if (pythagorean_quadruple(a, b, c, d))
        document.write("Yes");
    else
        document.write("No" );

</script>

Output: 

Yes

Time Complexity: O(1) 
Auxiliary Space: O(1)

References 
Wiki
mathworld