Puzzle | Who wins the race on a square field ABCD of 40 acres
Last Updated :
18 Jan, 2023
ABCD is a square field of 40 acres. The line BE is a straight path, and E is 110 yards from D. In a race Adam runs direct from A to D, but Brown has to start from B, go from B to E, and thence to D. Each keeps to a uniform speed throughout, and when Brown reaches E, Adams is 30 yards ahead of him. Which wins the race, and by how much?
Solution:
First step is to convert the area in acres to yards.
1 Acre is equal to 4840 square yards (yd²). To convert acres to square yards, multiply the acre value by 4840.
Area = 40*4840
= 193600 square yards.
Using area of square formula we can find the value of the side(s) of the square.
Area = S * S =193600
S = 440 yards
Side of the square is 440 yards.
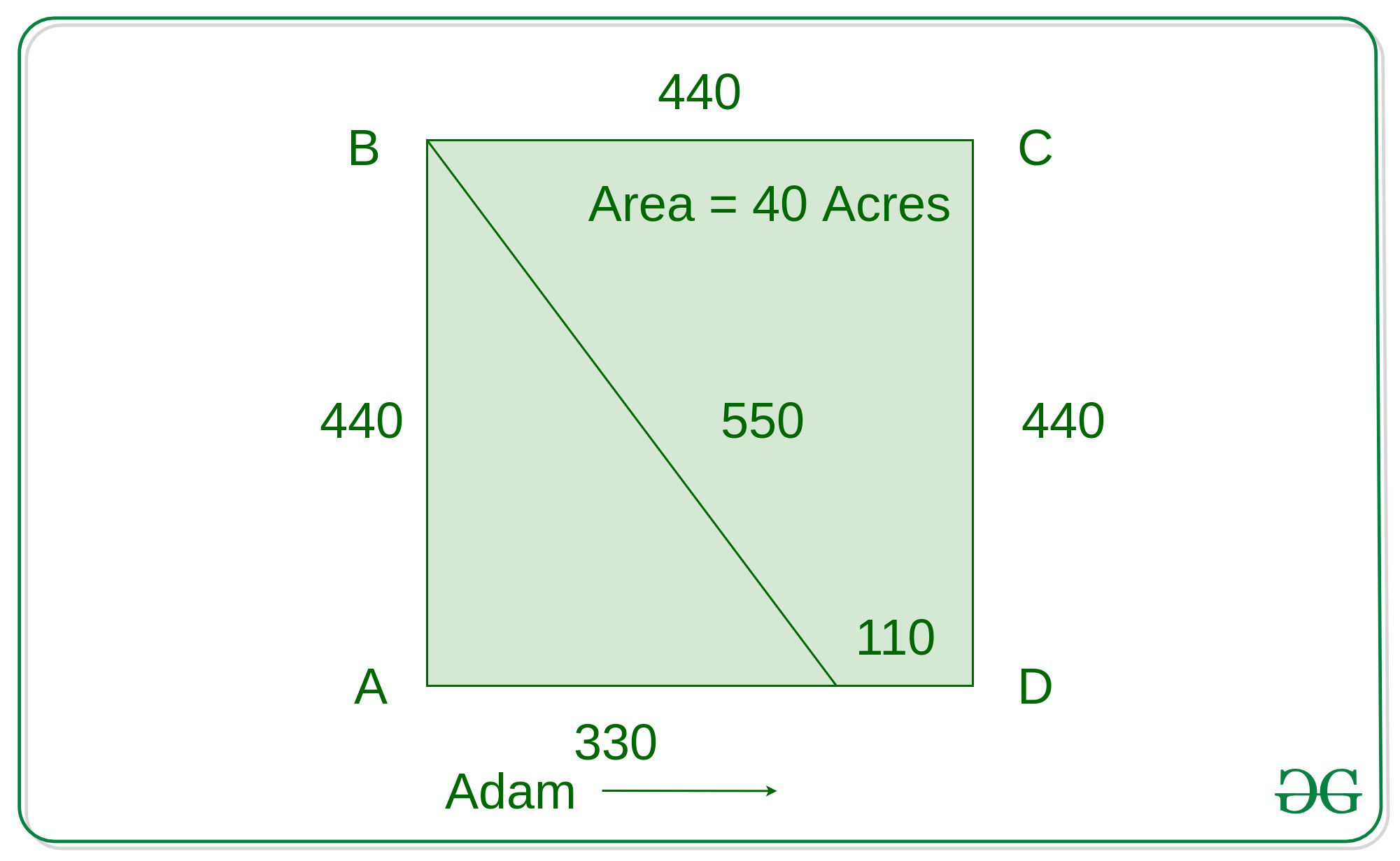
Each side of the field is 440 yards; BAE is a right-angled triangle, AE being 330 yards and BE 550 yards(Using Pythagoras Theorem).
AD = AE + ED
AD = 440 , ED = 110
440 = AD + 110
AE = 330
BAE is a right-angled triangle, applying Pythagoras theorem for the triangle BAE:
BE2 = AE2 + AB2
BE2 = 3302 + 4402
BE = 550
Assume Brown runs 550 yards in time “t” and reaches E while Adam runs 360 yards ( 330 + 30 ) in the same time and reaches a point F between E and D. The ratio of distances is proportional to ratio of speeds. The distance ran by Adam and Brown be D1 and D2 and speeds be S1 and S2 respectively.
D1 / D2 = 36 / 55 = S1 / S2
Speeds of Adam and Brown are 33k and 55k respectively, where k is a variable greater than zero.
Adam covers the remaining distance 80 ( 440 – 360 ) yards in 2.2/k units of time and Brown covers the remaining distance 110 (from E to D) in 2/k units of time.
As Brown takes less time than Adam so he wins the race.
Margin of distance =( Distance covered by Brown in 2 units of time starting from E – Distance covered by Adam in 2 units of time from F )
(Assuming k equals one)
Margin of distance = ( (55 * 2 ) – ( 36 *2 + 30))
= (110 – 102)
= 8 yards
Brown wins the race by 8 yards.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...