Puzzle | Two Brothers and Facebook

Sahil and Ritik are brothers. One day they were discussing who is smarter. But gradually the discussion turned into an argument. Mother came and tried to handle the situation. She gave them a problem to solve and the one who will solve the problem first, would be considered smarter than the other. The problem is :
In a group of 6 people, you might find some people are friends on Facebook, or you might find that no one is friend on Facebook. The brothers are supposed to prove that there is always a group of 3 people where either :
– All 3 people are mutual friends on Facebook.
– All 3 people are strangers (i.e, no one is friend on Facebook).
  Can you help the brothers to reach to the solution ?

Answer :
The problem can be visualised using graph theory. Imagine each person is the vertex of a graph. Represent 6 people using 6 vertices of the graph. Draw a blue line between people who are friends and a red line between people who are not friends.

Vertices representing persons..

From one vertex, there can be 0,1,2,3,4,5 blue lines which is accompanied by 5,4,3,2,1,0 red lines. From a vertex, draw lines to other vertices. The lines which are not blue must be red and vice-versa. The number of red lines and blue lines will always be 5. For example, if there is 2 red lines , then there must be 3 blue lines. Because of this, there will always be either 3+ blue lines or 3+ red lines.(i.e, either will be present for atleast 3 times). Consider both the cases separately.

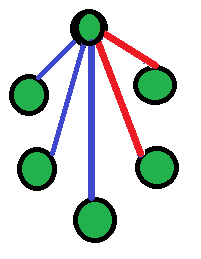
First consider that there are 3 red lines and 2 blue lines. The representation is shown in the figure as :

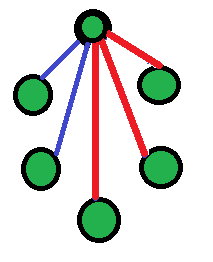
Look at the vertices which are connected by red lines. Look at the friends of this person. If none are friends, it means these are 3 mutual strangers(shown by red triangle).

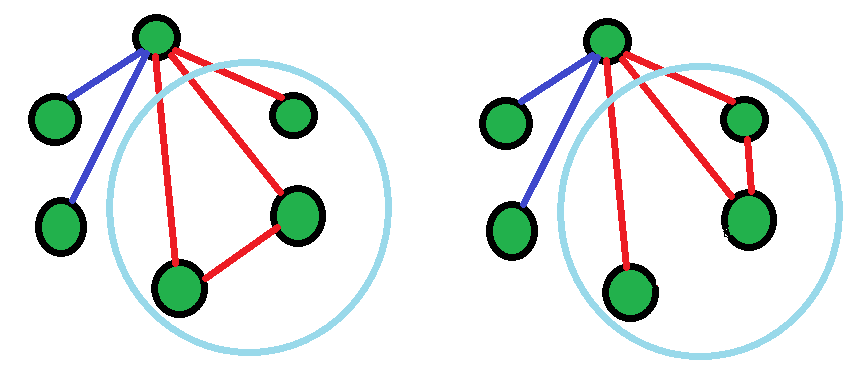
If any are friends, it means these are 3 mutual friends(shown by blue triangle).

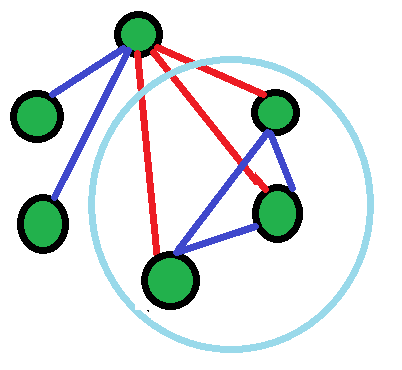
So, this proves that there are always atleast 3 mutual friends or atleast 3 strangers.
Same can be proven by taking the other case(i.e if we have 3 blue lines and 2 red lines).In that case there would be a blue triangle if there are atleast 3 friends and a red triangle if there are atleast 3 strangers.

References-Youtube-The Friendship Riddle