Puzzle 64 | Surround the Villages

In a district called Daulatpur, which is one of the best planned city in the world, there is a certain arrangements of villages. The arrangement adheres the following design patterns:

• All the boundaries of a villages are straight, and all the villages are surrounded by four such boundaries of the same length.
• The length of the line joining the non – adjacent points are equal.
• All the villages are divided into a group of three villages, having a common playground fully surrounded by one boundary of each villages.

Then, the villages are further categorized into category of special villages. The special villages have the property that area of one of the villages among their group is equal to sum of the area of the other two villages. You have been given that the boundaries of a village may vary from 1 km to 15 km in length.
Find out the sum of the area of the playgrounds for those group of villages which have been categorized into special villages.

Note: It’s given that for each set of boundaries of the villages, only one special group exists.

Solution: 114 Km^2 .

Explanation: In the above question, it’s given that the boundaries of the villages are straight, equal, and in four in number. The length of the line joining the non – adjacent points => the length of the diagonal of the polygon. As the sides and diagonals of the polygon are equal, this implies that polygon is a square. So , the whole district is collection of given triplets of villages, where area in between the squares is playground.

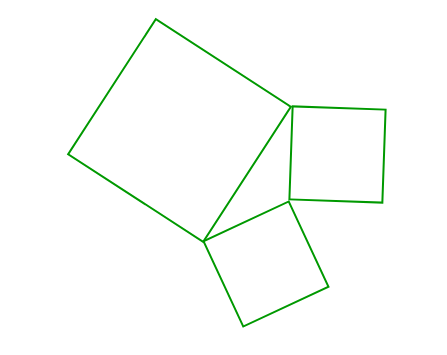
Now, the question says that the special villages are those villages having the sum of areas of two equal to the third one. Let the side of the villages in a triplet be a, b, & c respectively, which implies that
a^2 = b^2 + c^2

• Now, from 1 to 15 you have to find the Pythagorean triplets which are (3, 4, 5), (5, 12, 13),(9, 12, 15) and (6, 8, 10) respectively.
• As a^2 = b^2 + c^2, the triangular playgrounds are right angled. And as there are only one such special group.
• Therefore, the answer is (1/2 ) x 3 x 4 + (1/2) x 5 x 12 + (1/2) x 6 x 8 + (1/2) x 9 x 12= 114.

This puzzle is contributed by Praveer Satyam.