Puzzle | Supersonic Bee and Trains
Last Updated :
18 Jan, 2023
Puzzle: There are two trains(Train A and Train B) running on the same track towards each other at a speed of 100 km/hr. They enter a tunnel 200 km long at the same time. As soon as they enter, a supersonic bee flying at a rate of 1000 km/hr also enters the tunnel from one side (say Train A side). The bee flies towards the other Train B and as soon as it reaches the train B, it turns back and flies back to the Train A. This way it keeps flying to and fro between the Trains A and B. The trains collide after a certain point of time leading to a massive explosion. The task is to find the total distance travelled by the bee until the collision occurred.

Solution: This puzzle can be solved with the help of physics and observation.
- Speed of Train A and Train B = 100 km/hr
- Length of the tunnel = 200 km
- Since both the trains are travelling at the same speed, Hence they must have travelled equal distance before colliding, which means that they must have collided at the halfway of the tunnel.
- Therefore, distance travelled by each train before colliding = 100 km
- Time taken by each train to travel 100 km and collide = Distance/Speed = 100/100 = 1 hr
- Therefore the bee must have travelled for 1 hr before colliding with the trains.
- Hence distance travelled by the bee in 1 hr before colliding = Speed * Time = 1000 * 1 = 1000 km
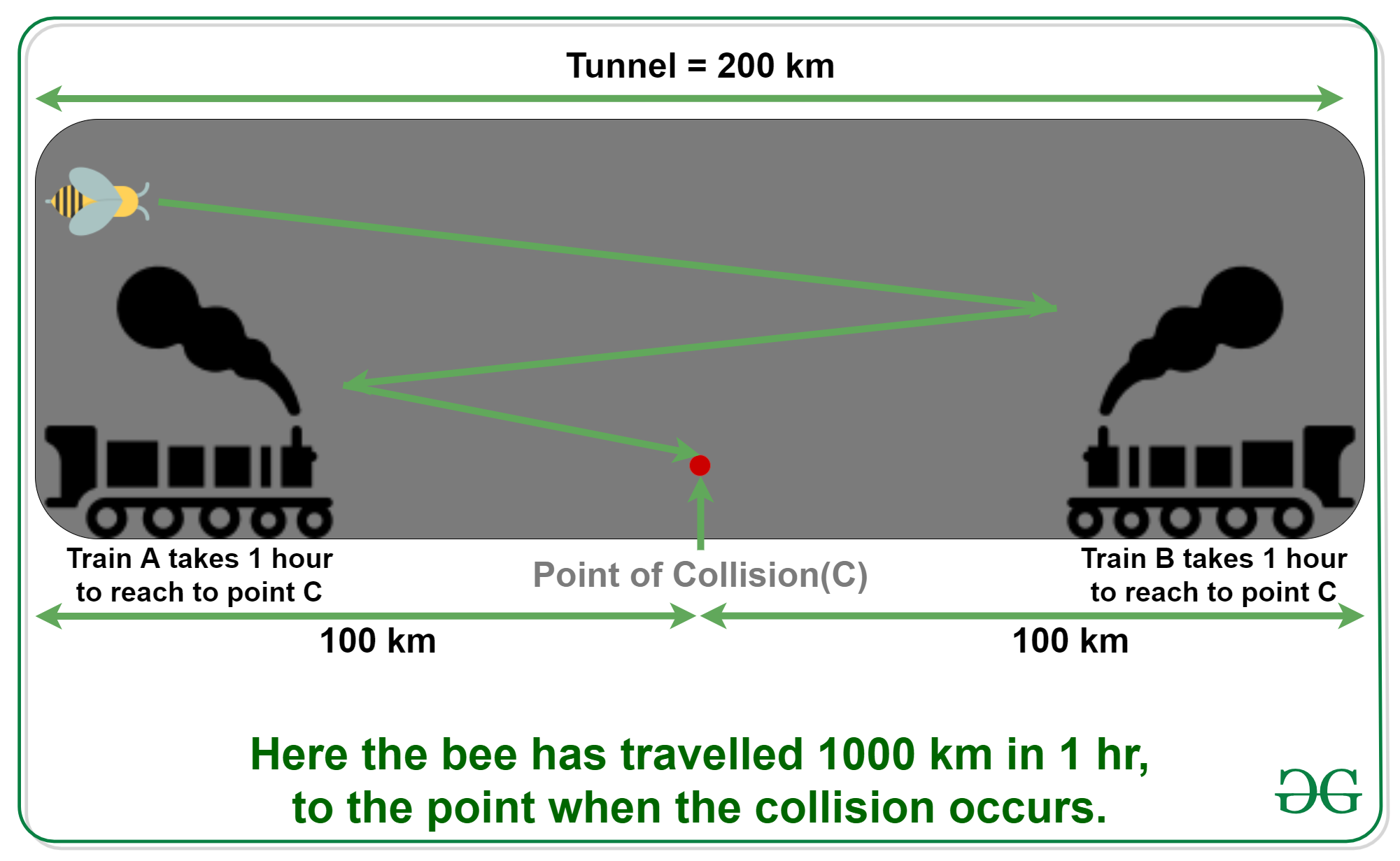
Therefore the bee must have travelled the said distance 1000 km until the collision.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...