Puzzle | Rat and Poisonous Milk Bottles
Last Updated :
21 Jul, 2023
You have
4 bottles of milk
. One of them is
poisonous
while the other 3 are non-poisonous. There is a rat which dies exactly after 10 hours of drinking the poisoned bottle. You have a clock that measures time only in hours. Suggest an
optimal strategy
to identify the poisoned bottle within 24 hours.

Solution 1:
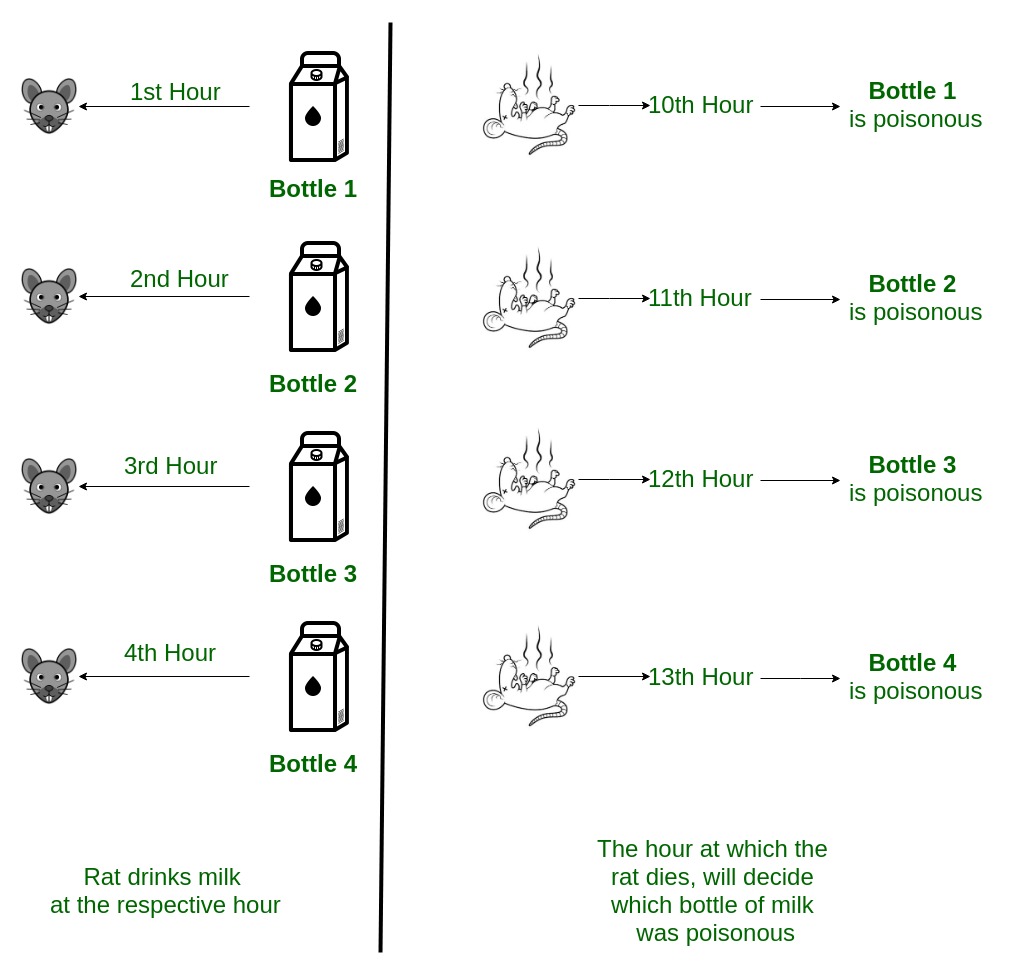
At the beginning of the first hour feed the rat the Ist bottle. At the start of 2nd-hour feed, the 2nd one and similarly at the start of 3rd-hour feed, the 3rd bottle. If the rat dies after exactly 10 hrs, the first bottle is poisonous. If it dies after 11 hours, 2nd one contains poison else the 3rd one is poisonous. In this way, after exactly 12 hours you would be able to determine the poisonous bottle.
Solution 2:
Step 1: Label the bottles from 1 to 4.
Step 2: Divide the bottles into two groups, A and B, with two bottles in each group. Label the groups as A and B.
Step 3: Take the rat and feed it with the milk from bottles 1 and 2.
Step 4: After 10 hours, observe the rat’s condition. If it dies, the poisoned bottle is either bottle 1 or 2. If the rat is still alive, proceed to step 5.
Step 5: Take the rat and feed it with the milk from bottle 1 (if the rat is still alive) and leave bottle 2 untouched. Step 6: After an additional 10 hours (a total of 20 hours since the start), observe the rat’s condition. If it dies, then bottle 1 is the poisoned one. If the rat is still alive, the poisoned bottle is bottle 3, as the rat has only consumed milk from bottle 1 and it survived.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...