Puzzle | Four Alternating Knights
Last Updated :
18 Jan, 2023
There are four knights on a 3 x 3 chessboard. The two white knights are at the two bottom corners, and the two black knights are at the upper two corners of the board. Find the shortest sequence of moves to achieve the final position as shown in the figure or prove that no such sequence exists.
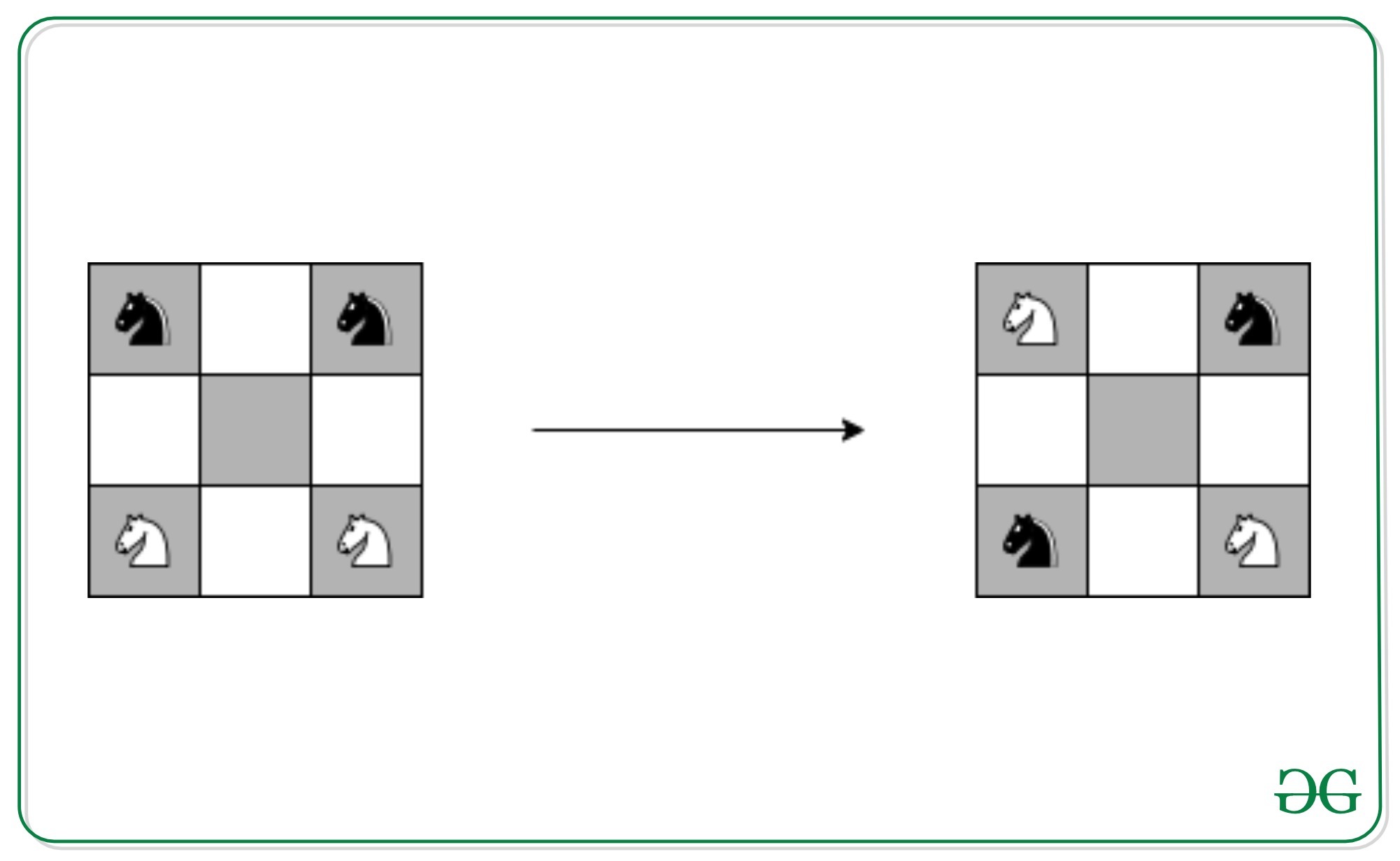
Solution:
A knight in a game of chess has L-shaped moves. So, it can occupy at most two different positions in a single move on a 3 x 3 board. Consider a graph where vertices represent the cell number and the edges between them represent, the moves that various knights can make.
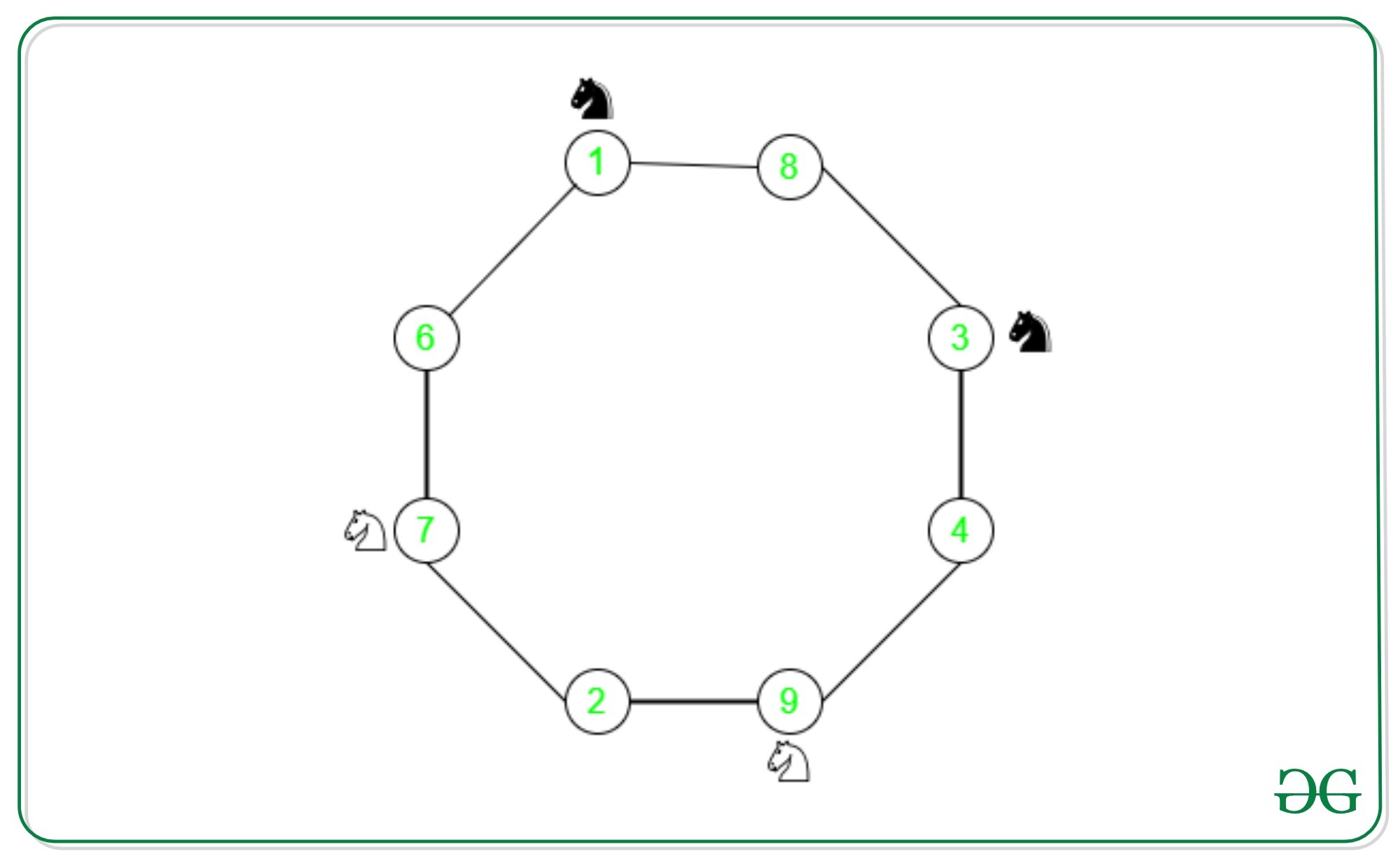
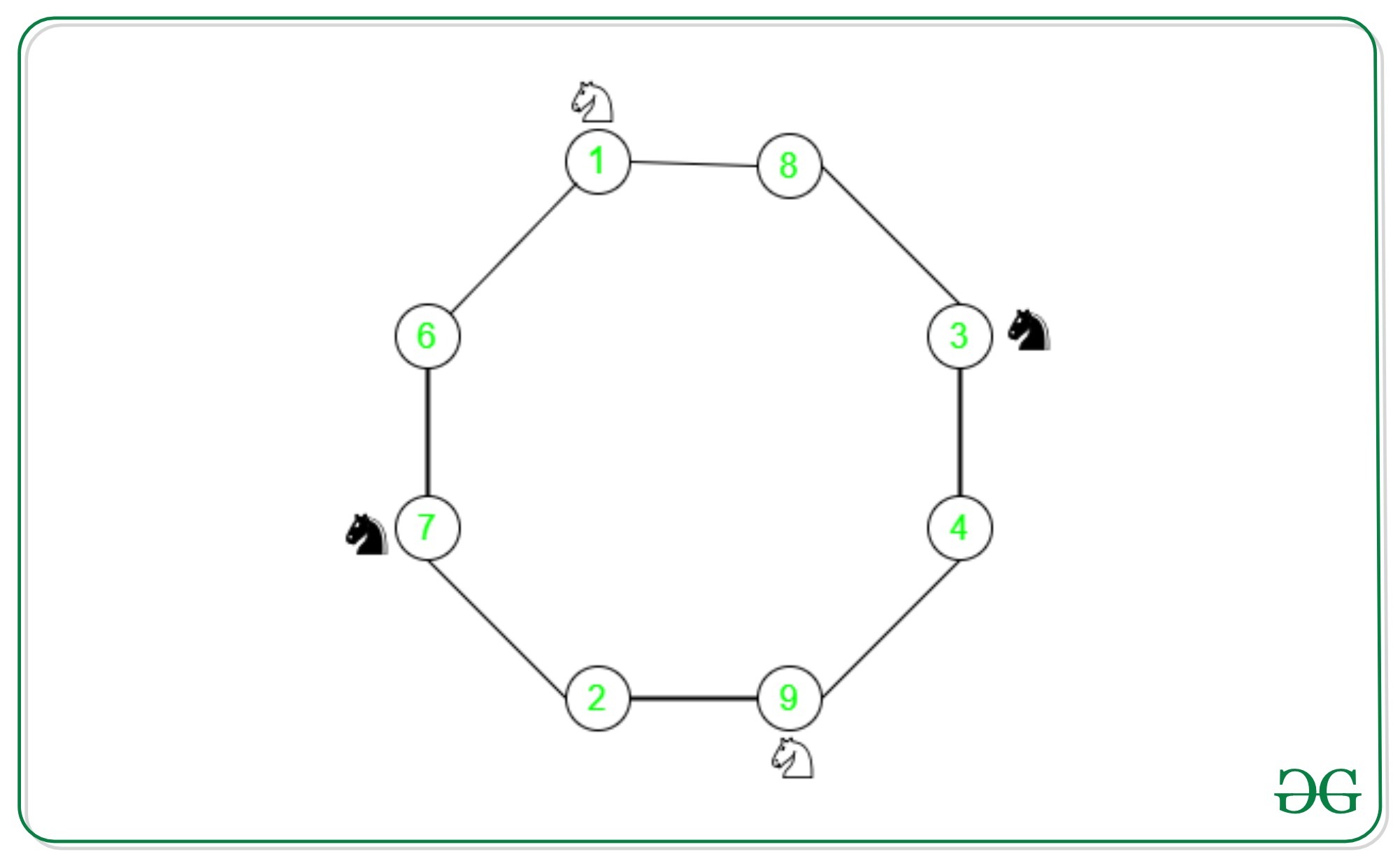
In this graph, we have two knights of the black color, followed by two knights of white color. Let’s consider knight at cell 1 moves to cell 6. Now to move to its final position cell 7, the knight at cell 7 should move to cell 2. However, its final position is cell 1 as shown. So the asked configuration is impossible to achieve. This is true for any sequence of moves, whether clockwise or counter-clockwise, as the ordering of the knights remains the same. However, the final configuration in question demands an alternating colored sequence of knights. So, this puzzle has no solution.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...