Puzzle | Find the overweight islander
Last Updated :
18 Jan, 2023
There are 12 men on an island. 11 weigh exactly the same, but one of them is slightly lighter or heavier. There is a seesaw to determine who is the odd one out. Find out the minimum number of times the seesaw will be used.
Solution: The minimum number of times seesaw will be needed is 3.
Explanation: A Divide and Conquer Approach can be used to solve this problem as follows.
Step 1: Divide the 12 men in 3 groups of 4 men each (A, B & C) and weigh the first group (A) against the second group (B).
Step 2: There are 2 possible outcomes.
- Case 1: They balance.
- Case 2: They don’t balance
Case 1
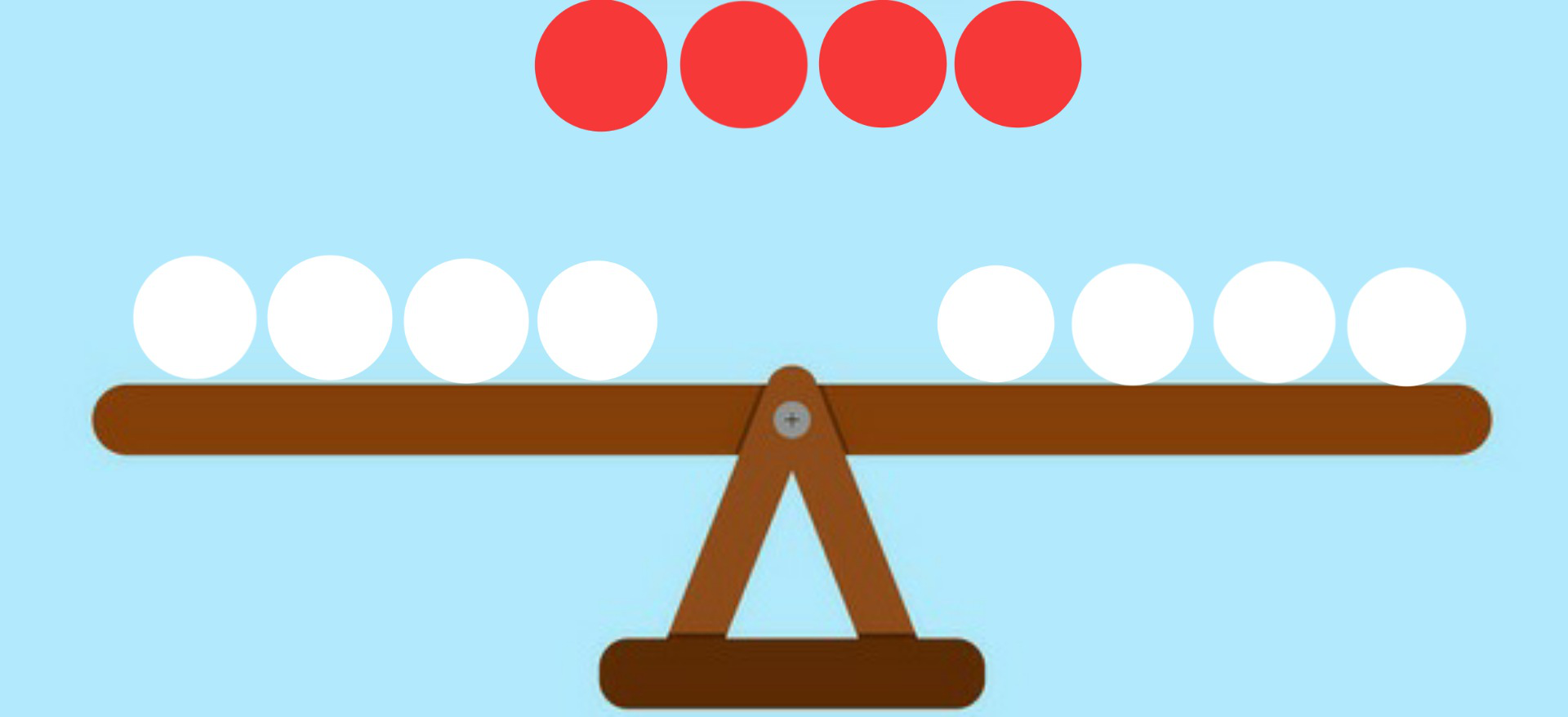
This means group C contains the odd one out. Now divide group C in two subgroups of 3 men (C1) and 1 men (C2), weigh the group C1 against 3 normal men from group A or group B and set aside group C2. Again there can be 3 possible outcomes here-
- The balls balance: It means men in group C2 is the odd one out and by comparing him against a normal man we can tell whether the man is heavier or lighter.
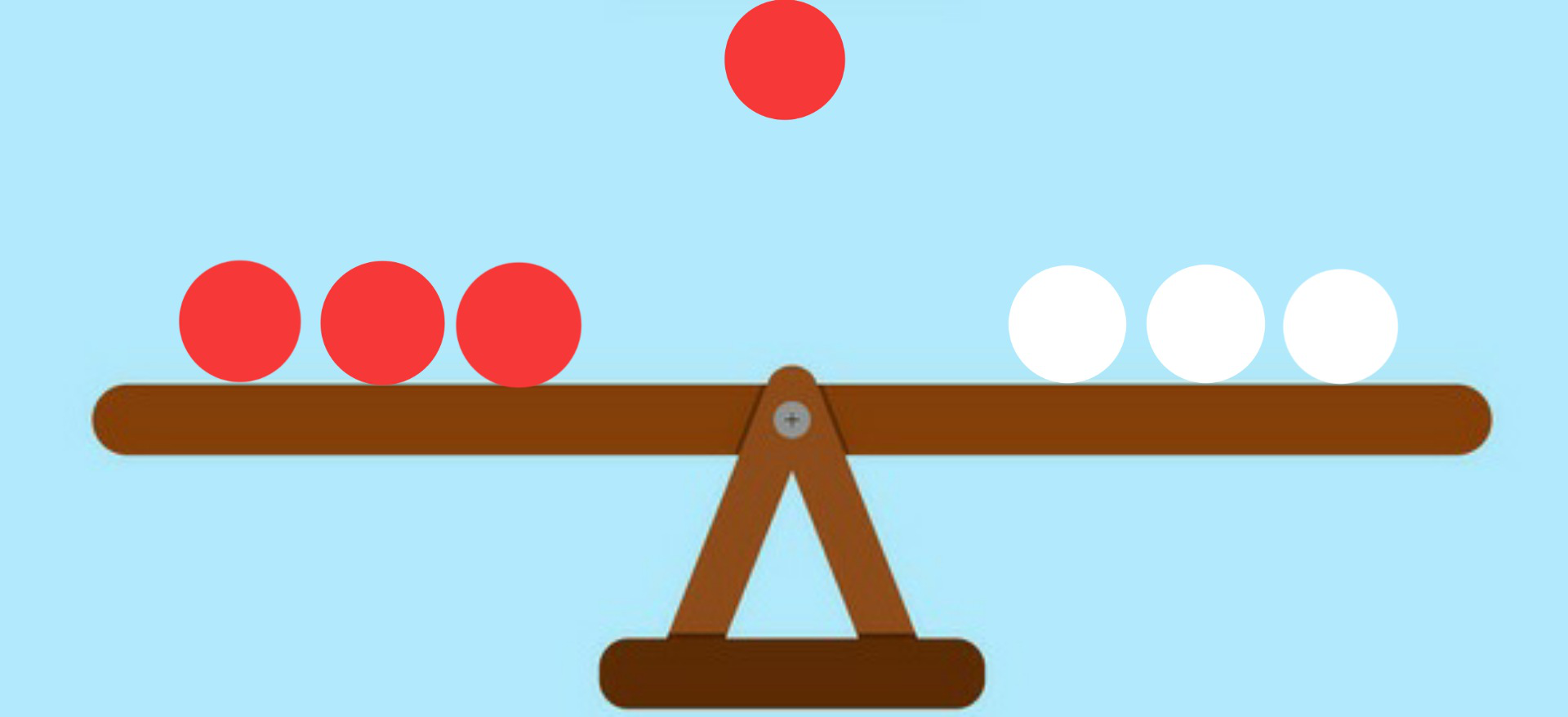
- C1 is lighter: If this occurs then by dividing the 3 men in three separate groups and weighing any two men will be enough to find odd one out and the man will be lighter.
- C1 is heavier: If this occurs the same dividing approach as of Sub-Case 1b will be enough to find odd one out and the man will be heavier.
Case 2

In this case there are total 8 suspects. Now divide this group in two subgroups of 5 men (A1) and 3 men (B1), Suppose subgroup A1 contains 4 heavier suspects and 1 lighter suspect and subgroup B1 contains 3 lighter suspects. Now compare subgroup A1 in such a way that on one side there are 2 heavier and 1 lighter suspects and on the other side there are the remaining 2 heavier suspects plus one normal men from group C. Again there can be 3 possible outcomes here:
- Balance: If they balance then the odd men is one of the three lighter suspects from group B1. Again by weighing the 2 amongst the remaining three lighter suspects will solve the problem and the man will be lighter.

- Weight shifts left: If the Weight shifts left. As because of the placement we can see that the 2 heavier suspects on the right are going upwards, so they can not be odd and hence they are of normal weight. Similarly, one lighter suspect on the left is going downwards, so he also can not be odd hence he also must be of normal weight. Finally, weighing the 2 remaining heavier suspects will solve the problem and the mean will be heavier.
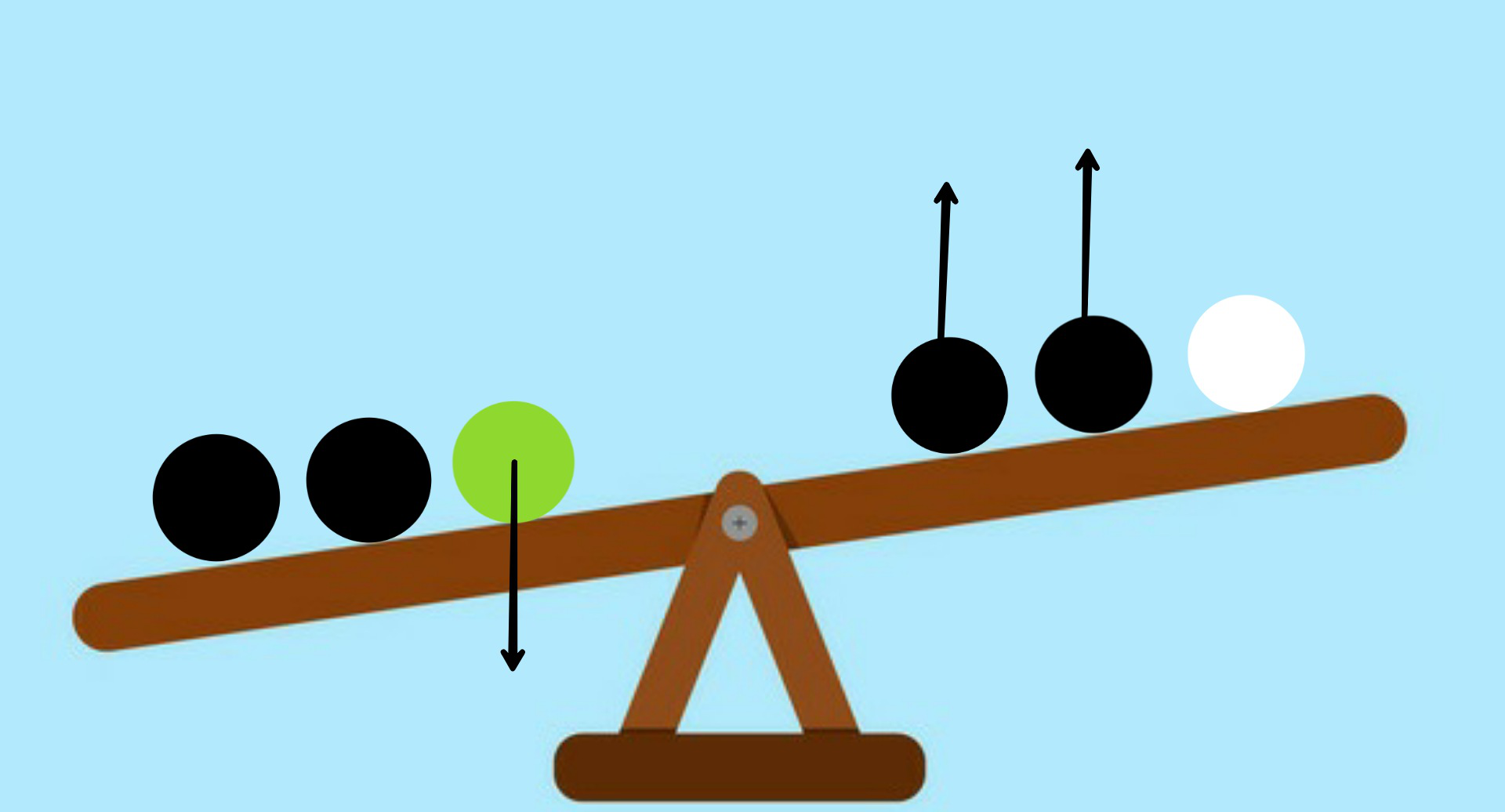
- Weight shifts right: If the Weight shifts right. Again according to the placement we can see that two of the heavier suspects on the left are going upwards and hence are of normal weights. Remaining three men are still suspects (1 lighter and 2 heavier). Now weigh the two heavier suspects against each other, if they balance then the lighter suspect is odd and will be lighter and if they don’t balance then whichever side goes downwards is the odd man and is heavier.

Reference: https://puzzling.stackexchange.com/questions/15426/brooklyn-nine-nine-riddle-weighing-islanders
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...