Puzzle | (Basketball shots)
Last Updated :
18 Jan, 2023
You have a basketball hoop and someone says that you can play one of two games.
Game1 : You get one shot to make the hoop.
Game2 : You get three shots and you have to make two of three shots.
If p is the probability of making a particular shot, for which values of p should you pick one game or the other?
Answer:
Probability of winning the Game 1:
The probability of winning game 1 is p, by definition.
Probability of winning the Game 2:
Let s(k, n) be the probability of making exactly k shots out of n.The probability of winning the Game 2 is the probability of making exactly two shots out of three OR making all three shots. In other words:
P(winning) = s(2, 3) + s(3, 3)
The probability of making all the three shots is:
s(3, 3) = 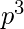
The probability of making exactly two shots is:
P(making 1 and 2, & missing 3) + P(making 1 and 3, & missing 2) + P(making 2 and 3, & missing 1)
= [p * p * (1-p)] + [p * (1-p) * p] + [(1-p) * p * p]
= 3*(1-p)*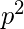
Adding these together, we get:
= 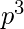 + 3(1-p)
+ 3(1-p)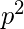 =
= 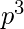 + 3
+ 3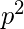 - 3
- 3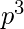 = 3
= 3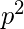 - 2
- 2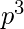
Which game you should play?
You should play Game 1 if P(Game 1) > P(Game 2):
p > 3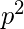 - 2
- 2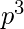 1 > 3p - 2
1 > 3p - 2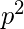 2
2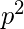 - 3p + 1 > 0
(2p - 1)(p - 1) > 0
- 3p + 1 > 0
(2p - 1)(p - 1) > 0
Both terms must be positive, or both must be negative, But we know p < 1, so p – 1 < 0. This means both terms must be negative.
2p - 1 < 0
2p < 1
p < 0.5
So, we should play Game 1 if 0 < p < 0.5 and Game 2 if 0.5 < p < 1.
If p = 0, 0.5, or 1 then P(Game 1) = P(Game 2), so it doesn't matter which game we play.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...