Puzzle | 50 red marbles and 50 blue marbles

Give two boxes B1 and B2 one have 50 red marbles and other have 50 blue marbles. A ball is selected randomly from any of the box and the task is to maximize the probability of selecting a red ball, by reshuffling marbles in both the boxes. Solution: Let P(R) be the probability of picking a red marble.

P(R) = P(B1) * P(B1 | J1) + P(B2) * P(B2 | J2)

Here, P(B1) and P(B2) refers to selecting B1 and B2 and the probability of selecting each box is 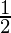J1 and J2 refers to number of total balls in B1 and B2 respectively. If we do not reshuffle any balls. Then

P(R) = ((1 / 2) * 1) + ((1 / 2) * 0) = 0.5

But, If we decrease the number of red balls in box B1 and increase the number of red balls in box B2 then the probability of getting a red ball will be maximized. Therefore, let us take 49 red marbles from B1 to B2 then there will be 1 red ball in B1 and 99 balls in B2 out of which 49 are red and 50 of them are blue in the second jar. Then

P (R) = ((1 / 2) * (1 / 1)) + ((1 / 2) * (49 / 99)) = 0.747474

Hence,

the maximum probability of choosing a red ball is 0.747474