Puzzle | 1000 light bulbs switched on/off by 1000 people passing by

Difficulty Level : Medium
Last Updated : 05 Jul, 2021

There are 1000 light bulbs and 1000 people. All light bulbs are initially off. Person 1 goes flipping light bulb 1, 2, 3, 4, … person 2 then flips 2, 4, 6, 8, … person 3 then 3, 6, 9, … etc until all 1000 persons have done this. What is the status of light bulbs 25, 93, 576, 132, 605, 26, 45, 37, 36 after all people have flipped their respective light bulbs? Is there a general solution to predict the status of a light bulb? How many light bulbs are on after all 1000 people have gone by?

Explanation: The key observations are:

Person 1 flips the light bulb 1, 2, 3, … which are multiples of 1.
Person 2 flips the light bulb 2, 4, 6, … which are multiples of 2.
Person 3 flips the light bulb 3, 6, 9, … which are multiples of 3.
Similarly, Person 1000 flips the light bulb 1000, which is a multiple of 1000.
From the above observations, we can say that person i will flip light bulbs which are multiples of i, $\forall i \in \{1, 2, 3, ..., 1000\}.$
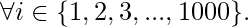
Thus, a light bulb j will be flipped by all persons for whom j is a multiple of their person number. In other words, light bulb j will be flipped by all people whose for person number i is a factor of j, $\forall i, j \in \{1, 2, 3, ..., 1000\}.$
Examples:
- (i) Light Bulb 10 will be flipped by persons 1, 2, 5, 10 whose person numbers are factors of 10.
- (ii) Light Bulb 12 will be flipped by persons 1, 2, 3, 4, 6, 12 whose person numbers are factors of 12.
Thus, light bulb 25 will be flipped by persons 1, 5, 25, so it will be flipped 3 times, which is odd and since initially, all bulbs were “off”, now light bulb 25 will be “on”.
The light bulb 93 will be flipped by persons 1, 3, 31, 93, so it will be flipped 4 times, which is even and since initially, all bulbs were “off”, now light bulb 93 will be “off”.
The light bulb 576 will be flipped by persons 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576, so it will be flipped 21 times, which is odd and since initially, all bulbs were “off”, now light bulb 576 will be “on”.
The light bulb 132 will be flipped by persons 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132, so it will be flipped 12 times, which is even and since initially, all bulbs were “off”, now light bulb 132 will be “off”.
The light bulb 605 will be flipped by persons 1, 5, 11, 55, 121, 605, so it will be flipped 6 times, which is even and since initially, all bulbs were “off”, now light bulb 605 will be “off”.
The light bulb 26 will be flipped by persons 1, 2, 13, 26, so it will be flipped 4 times, which is even and since initially, all bulbs were “off”, now light bulb 26 will be “off”.
The light bulb 45 will be flipped by persons 1, 3, 5, 9, 15, 45, so it will be flipped 6 times, which is even and since initially, all bulbs were “off”, now light bulb 45 will be “off”.
The light bulb 37, being the prime numbered bulb, will be flipped by persons 1, 37, so it will be flipped 2 times, which is even and since initially, all bulbs were “off”, now light bulb 37 will be “off”.
The light bulb 36 will be flipped by persons 1, 2, 3, 4, 6, 9, 12, 18, 36, so it will be flipped 9 times, which is odd and, since initially, all bulbs were “off”, now light bulb 36 will be “on”.

To find out the status of a given light bulb:
We count the number of factors of the light bulb number, and as per the above observations, if the number of factors is odd, then the light bulb will be “on”, and if it’s even, then it will be “off” in the end.
Algorithm to find how many light bulbs will be “on” in the end:
We count the factors of each number from 1 to 1000. If the number of factors for any number is odd, the corresponding light bulb is “on” so we update the result, and finally, print it.

Below is the code implementing the above algorithm.

C++

// C++ implementation of above approach
#include <iostream>
using namespace std;
 
int findOnBulbs(int numberOfBulbs)
{
    // initializing the result
    int onBulbs = 0;
     
    // to loop over all bulbs from 1 to numberOfBulbs
    int bulb = 1;
     
    // to loop over persons to check whether their person number
    int person = 1;
     
     
    // is a factor of light bulb number or not
    for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
         
        // inner loop to find factors of given bulb
        // to count the number of factors of a given bulb
        int factors = 0;
         
        for (person = 1; person * person <= numberOfBulbs; person++) {
             
            if (bulb % person == 0) // person is a factor
            {
                factors++;
                 
                // bulb != person*person
                if (bulb / person != person)
                {
                    factors++;
                }
            }
        }
         
        // if number of factors is odd, then the
        if (factors % 2 == 1)
         
        {
            // light bulb will be "on" in the end
            cout << "Light bulb "
                << bulb
                << " will be on"
                << "\n";
            onBulbs++;
        }
    }
     
     
    return onBulbs;
}
 
 
// Driver program to test above function
int main()
{
    // total number of light bulbs
    int numberOfBulbs = 1000;
     
    // to find number of on bulbs in
    // the end after all persons have
    // flipped the light bulbs
    int onBulbs = findOnBulbs(numberOfBulbs);
     
     
 
    cout << "Total "
        << onBulbs
        << " light bulbs will be on in the end out of "
        << numberOfBulbs
        << " light bulbs"
        << "\n";
    return 0;
}

Java

// Java implementation of the
// above given approach
public class GFG
{
 
static int findOnBulbs(int numberOfBulbs)
{
    // initializing the result
    int onBulbs = 0;
     
    // to loop over all bulbs from 1 to numberOfBulbs
    int bulb = 1;
     
    // to loop over persons to check whether their person number
    int person = 1;
     
     
    // is a factor of light bulb number or not
    for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
         
        // inner loop to find factors of given bulb
        // to count the number of factors of a given bulb
        int factors = 0;
         
        for (person = 1; person * person <= numberOfBulbs; person++) {
             
            if (bulb % person == 0) // person is a factor
            {
                factors++;
                 
                // bulb != person*person
                if (bulb / person != person)
                {
                    factors++;
                }
            }
        }
         
        // if number of factors is odd, then the
        if (factors % 2 == 1)
         
        {
            // light bulb will be "on" in the end
            System.out.println("Light bulb " + bulb + " will be on");
            onBulbs++;
        }
    }
     
     
    return onBulbs;
}
 
 
// Driver program to test above function
public static void main(String [] args)
{
    // total number of light bulbs
    int numberOfBulbs = 1000;
     
    // to find number of on bulbs in
    // the end after all persons have
    // flipped the light bulbs
    int onBulbs = findOnBulbs(numberOfBulbs);
     
     
 
    System.out.println("Total " + onBulbs
        + " light bulbs will be on in the end out of "
        + numberOfBulbs + " light bulbs");
}
 
// This code is contributed
// by Ryuga
}

Python3

# Python3 code implementing the
# given approach
 
def findOnBulbs(numberOfBulbs):
 
    # initializing the result
    onBulbs = 0
     
    # to loop over all bulbs from
    # 1 to numberOfBulbs
    bulb = 1
     
    # to loop over persons to check
    # whether their person number
    person = 1
     
    # Is a factor of light bulb number or not
    for bulb in range(1, numberOfBulbs + 1):
         
        # inner loop to find factors of
        # given bulb to count the number
        # of factors of a given bulb
        factors = 0
         
        for person in range(1, int(numberOfBulbs**(0.5)) + 1):
            if bulb % person == 0: # person is a factor
                factors += 1
                 
                # bulb != person*person
                if bulb // person != person:
                    factors += 1
                 
        # if number of factors is odd, then the
        if factors % 2 == 1:
         
            # light bulb will be "on" in the end
            print("Light bulb", bulb, "will be on")
            onBulbs += 1
         
    return onBulbs
 
# Driver Code
if __name__ == "__main__":
 
    # total number of light bulbs
    numberOfBulbs = 1000
     
    # to find number of on bulbs in
    # the end after all persons have
    # flipped the light bulbs
    onBulbs = findOnBulbs(numberOfBulbs)
     
    print("Total", onBulbs, "light bulbs will",
                     "be on in the end out of",
                  numberOfBulbs, "light bulbs")
     
# This code is contributed
# by Rituraj Jain

C#

// C# implementation of above approach
using System;
class GFG
{
 
static int findOnBulbs(int numberOfBulbs)
{
    // initializing the result
    int onBulbs = 0;
     
    // to loop over all bulbs from 1 to numberOfBulbs
    int bulb = 1;
     
    // to loop over persons to check whether their person number
    int person = 1;
     
     
    // is a factor of light bulb number or not
    for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
         
        // inner loop to find factors of given bulb
        // to count the number of factors of a given bulb
        int factors = 0;
         
        for (person = 1; person * person <= numberOfBulbs; person++) {
             
            if (bulb % person == 0) // person is a factor
            {
                factors++;
                 
                // bulb != person*person
                if (bulb / person != person)
                {
                    factors++;
                }
            }
        }
         
        // if number of factors is odd, then the
        if (factors % 2 == 1)
         
        {
            // light bulb will be "on" in the end
            Console.WriteLine("Light bulb " + bulb + " will be on");
            onBulbs++;
        }
    }
     
     
    return onBulbs;
}
 
 
// Driver program to test above function
public static void Main()
{
    // total number of light bulbs
    int numberOfBulbs = 1000;
     
    // to find number of on bulbs in
    // the end after all persons have
    // flipped the light bulbs
    int onBulbs = findOnBulbs(numberOfBulbs);
     
     
 
    Console.WriteLine("Total " + onBulbs
        + " light bulbs will be on in the end out of "
        + numberOfBulbs + " light bulbs");
}
}
 
// This code is contributed
// by Akanksha Rai

PHP

<?php
// PHP implementation of above approach
 
function findOnBulbs($numberOfBulbs)
{
    // initializing the result
    $onBulbs = 0;
     
    // to loop over all bulbs from
    // 1 to numberOfBulbs
    $bulb = 1;
     
    // to loop over persons to check
    // whether their person number
    $person = 1;
     
     
    // is a factor of light bulb number or not
    for ($bulb = 1;
         $bulb <= $numberOfBulbs; $bulb++)
    {
         
        // inner loop to find factors of given
        // bulb to count the number of factors
        // of a given bulb
        $factors = 0;
         
        for ($person = 1;
             $person * $person <= $numberOfBulbs; $person++)
        {
             
            if ($bulb % $person == 0) // person is a factor
            {
                $factors++;
                 
                // bulb != person*person
                if ($bulb / $person != $person)
                {
                    $factors++;
                }
            }
        }
         
        // if number of factors is odd, then the
        if ($factors % 2 == 1)
         
        {
            // light bulb will be "on" in the end
            echo "Light bulb " . $bulb .
                 " will be on" ."\n";
            $onBulbs++;
        }
    }
     
    return $onBulbs;
}
 
// Driver Code
 
// total number of light bulbs
$numberOfBulbs = 1000;
 
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
$onBulbs = findOnBulbs($numberOfBulbs);
 
echo "Total " . $onBulbs . " light bulbs will " .
     "be on in the end out of " . $numberOfBulbs .
                             " light bulbs" ."\n";
 
// This code is contributed by ita_c
?>

Javascript

<script>
// Javascript implementation of the
// above given approach
     
function findOnBulbs(numberOfBulbs)
{
    // initializing the result
    let onBulbs = 0;
      
    // to loop over all bulbs from 1 to numberOfBulbs
    let bulb = 1;
      
    // to loop over persons to check whether their person number
    let person = 1;
      
      
    // is a factor of light bulb number or not
    for (bulb = 1; bulb <= numberOfBulbs; bulb++) {
          
        // inner loop to find factors of given bulb
        // to count the number of factors of a given bulb
        let factors = 0;
          
        for (person = 1; person * person <= numberOfBulbs; person++) {
              
            if (bulb % person == 0) // person is a factor
            {
                factors++;
                  
                // bulb != person*person
                if (bulb / person != person)
                {
                    factors++;
                }
            }
        }
          
        // if number of factors is odd, then the
        if (factors % 2 == 1)
          
        {
            // light bulb will be "on" in the end
            document.write("Light bulb " + bulb + " will be on<br>");
            onBulbs++;
        }
    }
      
      
    return onBulbs;
}
 
// Driver program to test above function
// total number of light bulbs
let numberOfBulbs = 1000;
 
// to find number of on bulbs in
// the end after all persons have
// flipped the light bulbs
let onBulbs = findOnBulbs(numberOfBulbs);
 
 
 
document.write("Total " + onBulbs
                   + " light bulbs will be on in the end out of "
                   + numberOfBulbs + " light bulbs");
     
// This code is contributed by avanitrachhadiya2155
</script>

The previous program is written in O(n*sqrt(n)).

From observation, it is clear that whenever the number of factors is odd, the bulb will be on.
For any non-square number with each divisor, there is a corresponding quotient, so the number of factors will be even.
For every square number, when we divide it by its square root, the quotient will be the same number, i.e. its square root. So it has an odd number of factors.

Therefore, we can write an efficient code for this problem which computes in O(sqrt(n)).

C++

#include<iostream>
#include<math.h>
using namespace std;
 
int main()
{
    int numberOfBulbs = 1000;
    int root = sqrt(numberOfBulbs);
    for (int i = 1; i < root + 1; i++)
    {
        cout << "Light bulb " << (i * i)
             << " will be on" << endl;
    }
    cout << "Total " << root
         << " light bulbs will be on in the end out of "
         << numberOfBulbs << " light bulbs" << endl;
    return 0;
}
 
// This code is contributed by Apurvaraj

Java

import java.io.*;
 
class GFG {
     
    // Driver code  
    public static void main (String[] args) {
         
        int numberOfBulbs = 1000;
    int root = (int) Math.sqrt(numberOfBulbs);
    for (int i = 1; i < root + 1; i++)
    {
        System.out.println("Light bulb " + (i * i) +" will be on");
    }
      
    System.out.println("Total " + root
        + " light bulbs will be on in the end out of "
        + numberOfBulbs + " light bulbs");
         
    }
}
 
// This code is contributed b ab2127.

Python3

import math
root = int(math.sqrt(1000))
 
for i in range(1, root + 1):
    print("Light bulb %d will be on"%(i * i))
     
print("""Total %d light bulbs will be on
in the end out of 1000 light bulbs"""%root)

C#

using System;
using System.Collections.Generic;
 
class GFG
{
 
// Driver code   
public static void Main(String [] args)
{
    int numberOfBulbs = 1000;
    int root = (int) Math.Sqrt(numberOfBulbs);
    for (int i = 1; i < root + 1; i++)
    {
        Console.WriteLine("Light bulb " + (i * i) +" will be on");
    }
     
    Console.WriteLine("Total " + root
        + " light bulbs will be on in the end out of "
        + numberOfBulbs + " light bulbs");
}
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
     
        var numberOfBulbs = 1000;
        var root = parseInt( Math.sqrt(numberOfBulbs));
        for (i = 1; i < root + 1; i++) {
            document.write("Light bulb " + (i * i) + " will be on<br/>");
        }
 
        document.write(
                "Total " + root + " light bulbs will be on in the end out of "
                + numberOfBulbs + " light bulbs<br/>");
 
// This code is contributed by Rajput-Ji
</script>

Output:

Light bulb 1 will be on
Light bulb 4 will be on
Light bulb 9 will be on
Light bulb 16 will be on
Light bulb 25 will be on
Light bulb 36 will be on
Light bulb 49 will be on
Light bulb 64 will be on
Light bulb 81 will be on
Light bulb 100 will be on
Light bulb 121 will be on
Light bulb 144 will be on
Light bulb 169 will be on
Light bulb 196 will be on
Light bulb 225 will be on
Light bulb 256 will be on
Light bulb 289 will be on
Light bulb 324 will be on
Light bulb 361 will be on
Light bulb 400 will be on
Light bulb 441 will be on
Light bulb 484 will be on
Light bulb 529 will be on
Light bulb 576 will be on
Light bulb 625 will be on
Light bulb 676 will be on
Light bulb 729 will be on
Light bulb 784 will be on
Light bulb 841 will be on
Light bulb 900 will be on
Light bulb 961 will be on
Total 31 light bulbs will be on in the end out of 1000 light bulbs

My Personal Notes

Related Articles

Related Articles

Puzzle | 1000 light bulbs switched on/off by 1000 people passing by

C++

Java

Python3

C#

PHP

Javascript

C++

Java

Python3

C#

Javascript