Push Relabel Algorithm | Set 2 (Implementation)

We strongly recommend to refer below article before moving on to this article. 
Push Relabel Algorithm | Set 1 (Introduction and Illustration)

Problem Statement:

Given a graph that represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints:

1. Flow on an edge doesn’t exceed the given capacity of the edge.
2. Incoming flow is equal to outgoing flow for every vertex except s and t.

For example, consider the following graph from CLRS book.  

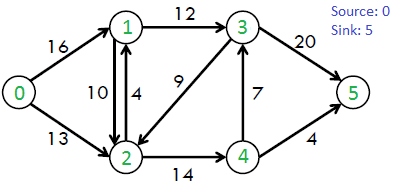
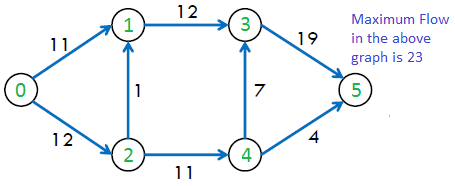
The maximum possible flow in the above graph is 23. 

Push-Relabel Algorithm 
1) Initialize PreFlow : Initialize Flows and Heights 

2) While it is possible to perform a Push() or Relabel() on a vertex
   // Or while there is a vertex that has excess flow
           Do Push() or Relabel()

// At this point all vertices have Excess Flow as 0 (Except source
// and sink)
3) Return flow.

Below are main operations performed in Push Relabel algorithm.  

There are three main operations in Push-Relabel Algorithm

1. Initialize PreFlow() It initializes heights and flows of all vertices. 

Preflow() 
1) Initialize height and flow of every vertex as 0.
2) Initialize height of source vertex equal to total 
   number of vertices in graph.
3) Initialize flow of every edge as 0.
4) For all vertices adjacent to source s, flow and  
   excess flow is equal to capacity initially.

2. Push() is used to make the flow from a node that has excess flow. If a vertex has excess flow and there is an adjacent with a smaller height (in the residual graph), we push the flow from the vertex to the adjacent with a lower height. The amount of pushed flow through the pipe (edge) is equal to the minimum of excess flow and capacity of the edge.

3. Relabel() operation is used when a vertex has excess flow and none of its adjacents is at the lower height. We basically increase the height of the vertex so that we can perform push(). To increase height, we pick the minimum height adjacent (in residual graph, i.e., an adjacent to whom we can add flow) and add 1 to it.

Implementation:

The following implementation uses the below structure for representing a flow network. 

struct Vertex 
{
   int h;      // Height of node
   int e_flow; // Excess Flow 
}

struct Edge 
{
   int u, v; // Edge is from u to v       
   int flow; // Current flow
   int capacity; 
}

class Graph 
{
   Edge edge[];   // Array of edges
   Vertex ver[];  // Array of vertices 
}

The below code uses the given graph itself as a flow network and residual graph. We have not created a separate graph for the residual graph and have used the same graph for simplicity.

Implementation:

C++

// C++ program to implement push-relabel algorithm for 
// getting maximum flow of graph 
#include <bits/stdc++.h> 
using namespace std; 
  
struct Edge 
{ 
    // To store current flow and capacity of edge 
    int flow, capacity; 
  
    // An edge u--->v has start vertex as u and end 
    // vertex as v. 
    int u, v; 
  
    Edge(int flow, int capacity, int u, int v) 
    { 
        this->flow = flow; 
        this->capacity = capacity; 
        this->u = u; 
        this->v = v; 
    } 
}; 
  
// Represent a Vertex 
struct Vertex 
{ 
    int h, e_flow; 
  
    Vertex(int h, int e_flow) 
    { 
        this->h = h; 
        this->e_flow = e_flow; 
    } 
}; 
  
// To represent a flow network 
class Graph 
{ 
    int V;    // No. of vertices 
    vector<Vertex> ver; 
    vector<Edge> edge; 
  
    // Function to push excess flow from u 
    bool push(int u); 
  
    // Function to relabel a vertex u 
    void relabel(int u); 
  
    // This function is called to initialize 
    // preflow 
    void preflow(int s); 
  
    // Function to reverse edge 
    void updateReverseEdgeFlow(int i, int flow); 
  
public: 
    Graph(int V);  // Constructor 
  
    // function to add an edge to graph 
    void addEdge(int u, int v, int w); 
  
    // returns maximum flow from s to t 
    int getMaxFlow(int s, int t); 
}; 
  
Graph::Graph(int V) 
{ 
    this->V = V; 
  
    // all vertices are initialized with 0 height 
    // and 0 excess flow 
    for (int i = 0; i < V; i++) 
        ver.push_back(Vertex(0, 0)); 
} 
  
void Graph::addEdge(int u, int v, int capacity) 
{ 
    // flow is initialized with 0 for all edge 
    edge.push_back(Edge(0, capacity, u, v)); 
} 
  
void Graph::preflow(int s) 
{ 
    // Making h of source Vertex equal to no. of vertices 
    // Height of other vertices is 0. 
    ver[s].h = ver.size(); 
  
    // 
    for (int i = 0; i < edge.size(); i++) 
    { 
        // If current edge goes from source 
        if (edge[i].u == s) 
        { 
            // Flow is equal to capacity 
            edge[i].flow = edge[i].capacity; 
  
            // Initialize excess flow for adjacent v 
            ver[edge[i].v].e_flow += edge[i].flow; 
  
            // Add an edge from v to s in residual graph with 
            // capacity equal to 0 
            edge.push_back(Edge(-edge[i].flow, 0, edge[i].v, s)); 
        } 
    } 
} 
  
// returns index of overflowing Vertex 
int overFlowVertex(vector<Vertex>& ver) 
{ 
    for (int i = 1; i < ver.size() - 1; i++) 
       if (ver[i].e_flow > 0) 
            return i; 
  
    // -1 if no overflowing Vertex 
    return -1; 
} 
  
// Update reverse flow for flow added on ith Edge 
void Graph::updateReverseEdgeFlow(int i, int flow) 
{ 
    int u = edge[i].v, v = edge[i].u; 
  
    for (int j = 0; j < edge.size(); j++) 
    { 
        if (edge[j].v == v && edge[j].u == u) 
        { 
            edge[j].flow -= flow; 
            return; 
        } 
    } 
  
    // adding reverse Edge in residual graph 
    Edge e = Edge(0, flow, u, v); 
    edge.push_back(e); 
} 
  
// To push flow from overflowing vertex u 
bool Graph::push(int u) 
{ 
    // Traverse through all edges to find an adjacent (of u) 
    // to which flow can be pushed 
    for (int i = 0; i < edge.size(); i++) 
    { 
        // Checks u of current edge is same as given 
        // overflowing vertex 
        if (edge[i].u == u) 
        { 
            // if flow is equal to capacity then no push 
            // is possible 
            if (edge[i].flow == edge[i].capacity) 
                continue; 
  
            // Push is only possible if height of adjacent 
            // is smaller than height of overflowing vertex 
            if (ver[u].h > ver[edge[i].v].h) 
            { 
                // Flow to be pushed is equal to minimum of 
                // remaining flow on edge and excess flow. 
                int flow = min(edge[i].capacity - edge[i].flow, 
                               ver[u].e_flow); 
  
                // Reduce excess flow for overflowing vertex 
                ver[u].e_flow -= flow; 
  
                // Increase excess flow for adjacent 
                ver[edge[i].v].e_flow += flow; 
  
                // Add residual flow (With capacity 0 and negative 
                // flow) 
                edge[i].flow += flow; 
  
                updateReverseEdgeFlow(i, flow); 
  
                return true; 
            } 
        } 
    } 
    return false; 
} 
  
// function to relabel vertex u 
void Graph::relabel(int u) 
{ 
    // Initialize minimum height of an adjacent 
    int mh = INT_MAX; 
  
    // Find the adjacent with minimum height 
    for (int i = 0; i < edge.size(); i++) 
    { 
        if (edge[i].u == u) 
        { 
            // if flow is equal to capacity then no 
            // relabeling 
            if (edge[i].flow == edge[i].capacity) 
                continue; 
  
            // Update minimum height 
            if (ver[edge[i].v].h < mh) 
            { 
                mh = ver[edge[i].v].h; 
  
                // updating height of u 
                ver[u].h = mh + 1; 
            } 
        } 
    } 
} 
  
// main function for printing maximum flow of graph 
int Graph::getMaxFlow(int s, int t) 
{ 
    preflow(s); 
  
    // loop until none of the Vertex is in overflow 
    while (overFlowVertex(ver) != -1) 
    { 
        int u = overFlowVertex(ver); 
        if (!push(u)) 
            relabel(u); 
    } 
  
    // ver.back() returns last Vertex, whose 
    // e_flow will be final maximum flow 
    return ver.back().e_flow; 
} 
  
// Driver program to test above functions 
int main() 
{ 
    int V = 6; 
    Graph g(V); 
  
    // Creating above shown flow network 
    g.addEdge(0, 1, 16); 
    g.addEdge(0, 2, 13); 
    g.addEdge(1, 2, 10); 
    g.addEdge(2, 1, 4); 
    g.addEdge(1, 3, 12); 
    g.addEdge(2, 4, 14); 
    g.addEdge(3, 2, 9); 
    g.addEdge(3, 5, 20); 
    g.addEdge(4, 3, 7); 
    g.addEdge(4, 5, 4); 
  
    // Initialize source and sink 
    int s = 0, t = 5; 
  
    cout << "Maximum flow is " << g.getMaxFlow(s, t); 
    return 0; 
} 

Java

import java.util.*;

// Class to represent an edge in the graph
class Edge {
    int flow, capacity, u, v;

    // Constructor for Edge class
    public Edge(int flow, int capacity, int u, int v) {
        this.flow = flow;
        this.capacity = capacity;
        this.u = u;
        this.v = v;
    }
}

// Class to represent a vertex in the graph
class Vertex {
    int h, e_flow;

    // Constructor for Vertex class
    public Vertex(int h, int e_flow) {
        this.h = h;
        this.e_flow = e_flow;
    }
}

// Class to represent a graph
class Graph {
    int V; // Number of vertices
    List<Vertex> ver; // List of vertices
    List<Edge> edge; // List of edges

    // Constructor for Graph class
    public Graph(int V) {
        this.V = V;
        ver = new ArrayList<>();
        edge = new ArrayList<>();

        // Initialize all vertices with 0 height and 0 excess flow
        for (int i = 0; i < V; i++)
            ver.add(new Vertex(0, 0));
    }

    // Method to add an edge to the graph
    public void addEdge(int u, int v, int capacity) {
        // Add an edge with 0 flow
        edge.add(new Edge(0, capacity, u, v));
    }

    // Method to initialize preflow
    public void preflow(int s) {
        // Set height of source equal to total number of vertices
        ver.get(s).h = ver.size();

        // Initialize flow of edges going from source
        for (int i = 0; i < edge.size(); i++) {
            if (edge.get(i).u == s) {
                // Flow is equal to capacity
                edge.get(i).flow = edge.get(i).capacity;

                // Initialize excess flow for adjacent vertex
                ver.get(edge.get(i).v).e_flow += edge.get(i).flow;

                // Add reverse edge in residual graph
                edge.add(new Edge(-edge.get(i).flow, 0, edge.get(i).v, s));
            }
        }
    }

    // Method to return index of overflowing vertex
    public int overFlowVertex() {
        for (int i = 1; i < ver.size() - 1; i++)
            if (ver.get(i).e_flow > 0)
                return i;

        // Return -1 if no overflowing vertex
        return -1;
    }

    // Method to update reverse flow for flow added on ith edge
    public void updateReverseEdgeFlow(int i, int flow) {
        int u = edge.get(i).v, v = edge.get(i).u;

        // Find edge
        for (int j = 0; j < edge.size(); j++) {
            if (edge.get(j).v == v && edge.get(j).u == u) {
                edge.get(j).flow -= flow;
                return;
            }
        }

        // Add reverse edge in residual graph
        Edge e = new Edge(0, flow, u, v);
        edge.add(e);
    }

    // Method to push flow from vertex u
    public boolean push(int u) {
        // Traverse through all edges to find an adjacent vertex
        for (int i = 0; i < edge.size(); i++) {
            // Check if u of current edge is same as given overflowing vertex
            if (edge.get(i).u == u) {
                // If flow is equal to capacity then no push is possible
                if (edge.get(i).flow == edge.get(i).capacity)
                    continue;

                // Push is only possible if height of adjacent vertex is smaller than height of overflowing vertex
                if (ver.get(u).h > ver.get(edge.get(i).v).h) {
                    // Flow to be pushed is equal to minimum of remaining flow on edge and excess flow
                    int flow = Math.min(edge.get(i).capacity - edge.get(i).flow,
                            ver.get(u).e_flow);

                    // Reduce excess flow for overflowing vertex
                    ver.get(u).e_flow -= flow;

                    // Increase excess flow for adjacent vertex
                    ver.get(edge.get(i).v).e_flow += flow;

                    // Increase flow along the edge
                    edge.get(i).flow += flow;

                    // Update reverse edge
                    updateReverseEdgeFlow(i, flow);

                    return true;
                }
            }
        }
        return false;
    }

    // Method to relabel vertex u
    public void relabel(int u) {
        int mh = Integer.MAX_VALUE;

        // Find adjacent vertex with minimum height
        for (int i = 0; i < edge.size(); i++) {
            if (edge.get(i).u == u) {
                // If flow is equal to capacity then no relabeling
                if (edge.get(i).flow == edge.get(i).capacity)
                    continue;

                // Update minimum height
                if (ver.get(edge.get(i).v).h < mh) {
                    mh = ver.get(edge.get(i).v).h;

                    // Update height of u
                    ver.get(u).h = mh + 1;
                }
            }
        }
    }

    // Method to get maximum flow from source s to sink t
    public int getMaxFlow(int s, int t) {
        preflow(s);

        // Loop until none of the vertices is in overflow
        while (overFlowVertex() != -1) {
            int u = overFlowVertex();
            if (!push(u))
                relabel(u);
        }

        // Return excess flow of sink
        return ver.get(ver.size() - 1).e_flow;
    }
}

public class Main {
    public static void main(String[] args) {
        int V = 6;
        Graph g = new Graph(V);

        // Creating the graph
        g.addEdge(0, 1, 16);
        g.addEdge(0, 2, 13);
        g.addEdge(1, 2, 10);
        g.addEdge(2, 1, 4);
        g.addEdge(1, 3, 12);
        g.addEdge(2, 4, 14);
        g.addEdge(3, 2, 9);
        g.addEdge(3, 5, 20);
        g.addEdge(4, 3, 7);
        g.addEdge(4, 5, 4);

        int s = 0, t = 5;

        // Print the maximum flow from source to sink
        System.out.println("Maximum flow is " + g.getMaxFlow(s, t));
    }
}

C#

// C# program to implement push-relabel algorithm for 
// getting maximum flow of graph
using System;
using System.Collections.Generic;
using System.Collections;
using System.Linq;

class Edge 
{ 
    public int flow;
    public int capacity;
    public int u;
    public int v;
    
    public Edge(int flow,int capacity,int u,int v) 
    { 
        this.flow = flow; 
        this.capacity = capacity; 
        this.u = u; 
        this.v = v; 
    } 
} 
  
// Represent a Vertex 
class Vertex 
{ 
    public int h;
    public int e_flow;
    public Vertex(int h,int e_flow) 
    { 
        this.h = h; 
        this.e_flow = e_flow; 
    } 
}
  
// To represent a flow network 
class Graph 
{ 
    
    public int V;    // No. of vertices 
    public List<Vertex> ver; 
    public List<Edge> edge; 
    public Graph(int V) 
    { 
        this.V = V; 
        ver = new List<Vertex>();
        edge = new List<Edge>();
        // all vertices are initialized with 0 height 
        // and 0 excess flow 
        for (int i = 0; i < V; i++) 
            ver.Add(new Vertex(0, 0)); 
    }
    
    public void addEdge(int u,int v,int capacity) 
    { 
        // flow is initialized with 0 for all edge 
        edge.Add(new Edge(0, capacity, u, v)); 
    } 


    public void preflow(int s) 
    { 
        // Making h of source Vertex equal to no. of vertices 
        // Height of other vertices is 0. 
        ver[s].h = ver.Count; 

        // 
        for (int i = 0; i < edge.Count; i++) 
        { 
            // If current edge goes from source 
            if (edge[i].u == s) 
            { 
                // Flow is equal to capacity 
                edge[i].flow = edge[i].capacity; 

                // Initialize excess flow for adjacent v 
                ver[edge[i].v].e_flow += edge[i].flow; 

                // Add an edge from v to s in residual graph with 
                // capacity equal to 0 
                edge.Add(new Edge(-edge[i].flow, 0, edge[i].v, s)); 
            } 
        } 
    } 
    
    // returns index of overflowing Vertex 
    public int overFlowVertex() 
    { 
        for (int i = 1; i < ver.Count - 1; i++) 
           if (ver[i].e_flow > 0) 
                return i; 

        // -1 if no overflowing Vertex 
        return -1; 
    } 
    

    // Update reverse flow for flow added on ith Edge 
    public void updateReverseEdgeFlow(int i,int  flow) 
    { 
        int u = edge[i].v;
        int v = edge[i].u; 

        for (int j = 0; j < edge.Count; j++) 
        { 
            if (edge[j].v == v && edge[j].u == u) 
            { 
                edge[j].flow -= flow; 
                return; 
            } 
        } 

        // adding reverse Edge in residual graph 
        Edge e = new Edge(0, flow, u, v); 
        edge.Add(e); 
    } 

    // To push flow from overflowing vertex u 
    public bool push(int u) 
    { 
        // Traverse through all edges to find an adjacent (of u) 
        // to which flow can be pushed 
        for (int i = 0; i < edge.Count; i++) 
        { 
            // Checks u of current edge is same as given 
            // overflowing vertex 
            if (edge[i].u == u) 
            { 
                // if flow is equal to capacity then no push 
                // is possible 
                if (edge[i].flow == edge[i].capacity) 
                    continue; 

                // Push is only possible if height of adjacent 
                // is smaller than height of overflowing vertex 
                if (ver[u].h > ver[edge[i].v].h) 
                { 
                    // Flow to be pushed is equal to minimum of 
                    // remaining flow on edge and excess flow. 
                    int flow = Math.Min(edge[i].capacity - edge[i].flow, 
                                   ver[u].e_flow); 

                    // Reduce excess flow for overflowing vertex 
                    ver[u].e_flow -= flow; 

                    // Increase excess flow for adjacent 
                    ver[edge[i].v].e_flow += flow; 

                    // Add residual flow (With capacity 0 and negative 
                    // flow) 
                    edge[i].flow += flow; 

                    updateReverseEdgeFlow(i, flow); 

                    return true; 
                } 
            } 
        } 
        return false; 
    } 
    
    
    // function to relabel vertex u 
    public void relabel(int u) 
    { 
        // Initialize minimum height of an adjacent 
        int mh = 2100000; 

        // Find the adjacent with minimum height 
        for (int i = 0; i < edge.Count; i++) 
        { 
            if (edge[i].u == u) 
            { 
                // if flow is equal to capacity then no 
                // relabeling 
                if (edge[i].flow == edge[i].capacity) 
                    continue; 

                // Update minimum height 
                if (ver[edge[i].v].h < mh) 
                { 
                    mh = ver[edge[i].v].h; 

                    // updating height of u 
                    ver[u].h = mh + 1; 
                } 
            } 
        } 
    } 
    
    // main function for printing maximum flow of graph 
    public int getMaxFlow(int s,int  t) 
    { 
        preflow(s); 

        // loop until none of the Vertex is in overflow 
        while (overFlowVertex() != -1) 
        { 
            int u = overFlowVertex(); 
            if (!push(u)) 
                relabel(u); 
        } 

        // ver.back() returns last Vertex, whose 
        // e_flow will be final maximum flow 
        return ver[ver.Count-1].e_flow; 
    } 
} 
  



class HelloWorld {

    
    static void Main() {

        // Driver program to test above functions 
        int V = 6; 
        Graph g = new Graph(V);

        // Creating above shown flow network 
        g.addEdge(0, 1, 16); 
        g.addEdge(0, 2, 13); 
        g.addEdge(1, 2, 10); 
        g.addEdge(2, 1, 4); 
        g.addEdge(1, 3, 12); 
        g.addEdge(2, 4, 14); 
        g.addEdge(3, 2, 9); 
        g.addEdge(3, 5, 20); 
        g.addEdge(4, 3, 7); 
        g.addEdge(4, 5, 4); 

        // Initialize source and sink 
        int s = 0, t = 5; 

        Console.WriteLine("Maximum flow is " + g.getMaxFlow(s, t)); 
    }
}

// The code is contributed by Arushi jindal. 

Javascript

// javascript program to implement push-relabel algorithm for 
// getting maximum flow of graph 
class Edge 
{ 
    constructor(flow, capacity, u, v) 
    { 
        this.flow = flow; 
        this.capacity = capacity; 
        this.u = u; 
        this.v = v; 
    } 
} 
  
// Represent a Vertex 
class Vertex 
{ 
  
    constructor(h, e_flow) 
    { 
        this.h = h; 
        this.e_flow = e_flow; 
    } 
}
  
// To represent a flow network 
class Graph 
{ 
    
    // int V;    // No. of vertices 
    // vector<Vertex> ver; 
    // vector<Edge> edge; 
    constructor(V) 
    { 
        this.V = V; 
        this.edge = new Array();
        this.ver = new Array();
        // all vertices are initialized with 0 height 
        // and 0 excess flow 
        for (let i = 0; i < V; i++) 
            this.ver.push(new Vertex(0, 0)); 
    }
    
    addEdge(u, v, capacity) 
    { 
        // flow is initialized with 0 for all edge 
        this.edge.push(new Edge(0, capacity, u, v)); 
    } 


    preflow(s) 
    { 
        // Making h of source Vertex equal to no. of vertices 
        // Height of other vertices is 0. 
        this.ver[s].h = this.ver.length; 

        // 
        for (let i = 0; i < this.edge.length; i++) 
        { 
            // If current edge goes from source 
            if (this.edge[i].u == s) 
            { 
                // Flow is equal to capacity 
                this.edge[i].flow = this.edge[i].capacity; 

                // Initialize excess flow for adjacent v 
                this.ver[this.edge[i].v].e_flow += this.edge[i].flow; 

                // Add an edge from v to s in residual graph with 
                // capacity equal to 0 
                this.edge.push(new Edge(-this.edge[i].flow, 0, this.edge[i].v, s)); 
            } 
        } 
    } 
    
    // returns index of overflowing Vertex 
    overFlowVertex() 
    { 
        for (let i = 1; i < this.ver.length - 1; i++) 
           if (this.ver[i].e_flow > 0) 
                return i; 

        // -1 if no overflowing Vertex 
        return -1; 
    } 
    

    // Update reverse flow for flow added on ith Edge 
    updateReverseEdgeFlow(i, flow) 
    { 
        let u = this.edge[i].v;
        let v = this.edge[i].u; 

        for (let j = 0; j < this.edge.length; j++) 
        { 
            if (this.edge[j].v == v && this.edge[j].u == u) 
            { 
                this.edge[j].flow -= flow; 
                return; 
            } 
        } 

        // adding reverse Edge in residual graph 
        let e = new Edge(0, flow, u, v); 
        this.edge.push(e); 
    } 

    // To push flow from overflowing vertex u 
    push(u) 
    { 
        // Traverse through all edges to find an adjacent (of u) 
        // to which flow can be pushed 
        for (let i = 0; i < this.edge.length; i++) 
        { 
            // Checks u of current edge is same as given 
            // overflowing vertex 
            if (this.edge[i].u == u) 
            { 
                // if flow is equal to capacity then no push 
                // is possible 
                if (this.edge[i].flow == this.edge[i].capacity) 
                    continue; 

                // Push is only possible if height of adjacent 
                // is smaller than height of overflowing vertex 
                if (this.ver[u].h > this.ver[this.edge[i].v].h) 
                { 
                    // Flow to be pushed is equal to minimum of 
                    // remaining flow on edge and excess flow. 
                    let flow = Math.min(this.edge[i].capacity - this.edge[i].flow, 
                                   this.ver[u].e_flow); 

                    // Reduce excess flow for overflowing vertex 
                    this.ver[u].e_flow -= flow; 

                    // Increase excess flow for adjacent 
                    this.ver[this.edge[i].v].e_flow += flow; 

                    // Add residual flow (With capacity 0 and negative 
                    // flow) 
                    this.edge[i].flow += flow; 

                    this.updateReverseEdgeFlow(i, flow); 

                    return true; 
                } 
            } 
        } 
        return false; 
    } 
    
    
    // function to relabel vertex u 
    relabel(u) 
    { 
        // Initialize minimum height of an adjacent 
        let mh = 2100000; 

        // Find the adjacent with minimum height 
        for (let i = 0; i < this.edge.length; i++) 
        { 
            if (this.edge[i].u == u) 
            { 
                // if flow is equal to capacity then no 
                // relabeling 
                if (this.edge[i].flow == this.edge[i].capacity) 
                    continue; 

                // Update minimum height 
                if (this.ver[this.edge[i].v].h < mh) 
                { 
                    mh = this.ver[this.edge[i].v].h; 

                    // updating height of u 
                    this.ver[u].h = mh + 1; 
                } 
            } 
        } 
    } 
    
    // main function for printing maximum flow of graph 
    getMaxFlow(s, t) 
    { 
        this.preflow(s); 

        // loop until none of the Vertex is in overflow 
        while (this.overFlowVertex() != -1) 
        { 
            let u = this.overFlowVertex(); 
            if (!this.push(u)) 
                this.relabel(u); 
        } 

        // ver.back() returns last Vertex, whose 
        // e_flow will be final maximum flow 
        return this.ver[this.ver.length-1].e_flow; 
    } 
} 
  

  

  

  

  

  

  

  

  
// Driver program to test above functions 
let V = 6; 
let g = new Graph(V);

// Creating above shown flow network 
g.addEdge(0, 1, 16); 
g.addEdge(0, 2, 13); 
g.addEdge(1, 2, 10); 
g.addEdge(2, 1, 4); 
g.addEdge(1, 3, 12); 
g.addEdge(2, 4, 14); 
g.addEdge(3, 2, 9); 
g.addEdge(3, 5, 20); 
g.addEdge(4, 3, 7); 
g.addEdge(4, 5, 4); 

// Initialize source and sink 
let s = 0, t = 5; 

console.log("Maximum flow is " + g.getMaxFlow(s, t)); 

// The code is contributed by Nidhi goel. 

Python3

# python program to implement push-relabel algorithm for 
# getting maximum flow of graph 
class Edge: 
    
    def __init__(self, flow, capacity, u, v):
        self.flow = flow
        self.capacity = capacity
        self.u = u
        self.v = v

# Represent a Vertex 
class Vertex:
  
    def __init__(self, h, e_flow):
        self.h = h
        self.e_flow = e_flow

        
# To represent a flow network 
class Graph:
    
    # int V;    # No. of vertices 
    # vector<Vertex> ver; 
    # vector<Edge> edge; 
    def __init__(self, V):
        
        self.V = V; 
        self.edge = []
        self.ver = []
        # all vertices are initialized with 0 height 
        # and 0 excess flow 
        for i in range(V):
            self.ver.append(Vertex(0, 0))
    
    def addEdge(self, u, v, capacity):
        # flow is initialized with 0 for all edge 
        self.edge.append(Edge(0, capacity, u, v))


    def preflow(self, s):
        
        # Making h of source Vertex equal to no. of vertices 
        # Height of other vertices is 0. 
        self.ver[s].h = len(self.ver); 

        for i in range(len(self.edge)): 
            
            # If current edge goes from source 
            if (self.edge[i].u == s):
                # Flow is equal to capacity 
                self.edge[i].flow = self.edge[i].capacity

                # Initialize excess flow for adjacent v 
                self.ver[self.edge[i].v].e_flow += self.edge[i].flow

                # Add an edge from v to s in residual graph with 
                # capacity equal to 0 
                self.edge.append(Edge(-self.edge[i].flow, 0, self.edge[i].v, s))
                

    # returns index of overflowing Vertex 
    def overFlowVertex(self):
        
        for i in range(1, len(self.ver)-1): 
            
            if(self.ver[i].e_flow > 0):
                return i

        # -1 if no overflowing Vertex 
        return -1
    

    # Update reverse flow for flow added on ith Edge 
    def updateReverseEdgeFlow(self, i, flow):
        
        u = self.edge[i].v
        v = self.edge[i].u 

        for j in range(0, len(self.edge)): 
            if (self.edge[j].v == v and self.edge[j].u == u):
                self.edge[j].flow -= flow
                return

        # adding reverse Edge in residual graph 
        e = Edge(0, flow, u, v)
        self.edge.append(e)
        

    # To push flow from overflowing vertex u 
    def push(self, u): 
        
        # Traverse through all edges to find an adjacent (of u) 
        # to which flow can be pushed 
        for i in range(0, len(self.edge)): 
            
            # Checks u of current edge is same as given 
            # overflowing vertex 
            if (self.edge[i].u == u):
                # if flow is equal to capacity then no push 
                # is possible 
                if (self.edge[i].flow == self.edge[i].capacity):
                    continue; 

                # Push is only possible if height of adjacent 
                # is smaller than height of overflowing vertex 
                if (self.ver[u].h > self.ver[self.edge[i].v].h):
                    
                    # Flow to be pushed is equal to minimum of 
                    # remaining flow on edge and excess flow. 
                    flow = min(self.edge[i].capacity - self.edge[i].flow, self.ver[u].e_flow)

                    # Reduce excess flow for overflowing vertex 
                    self.ver[u].e_flow -= flow; 

                    # Increase excess flow for adjacent 
                    self.ver[self.edge[i].v].e_flow += flow; 

                    # Add residual flow (With capacity 0 and negative 
                    # flow) 
                    self.edge[i].flow += flow; 

                    self.updateReverseEdgeFlow(i, flow); 

                    return True; 

        return False;  
    
    
    # function to relabel vertex u 
    def relabel(self, u):
        # Initialize minimum height of an adjacent 
        mh = 2100000

        # Find the adjacent with minimum height 
        for i in range(len(self.edge)):  
            if (self.edge[i].u == u):
                
                # if flow is equal to capacity then no 
                # relabeling 
                if (self.edge[i].flow == self.edge[i].capacity):
                    continue; 

                # Update minimum height 
                if (self.ver[self.edge[i].v].h < mh):
                    mh = self.ver[self.edge[i].v].h; 

                    # updating height of u 
                    self.ver[u].h = mh + 1; 

    
    # main function for printing maximum flow of graph 
    def getMaxFlow(self, s, t):
        
        self.preflow(s); 

        # loop until none of the Vertex is in overflow 
        while (self.overFlowVertex() != -1):
            
            u = self.overFlowVertex(); 
            if (self.push(u) == False):
                self.relabel(u); 

        # ver.back() returns last Vertex, whose 
        # e_flow will be final maximum flow 
        return self.ver[len(self.ver)-1].e_flow

    
# Driver program to test above functions 
V = 6; 
g = Graph(V);

# Creating above shown flow network 
g.addEdge(0, 1, 16); 
g.addEdge(0, 2, 13); 
g.addEdge(1, 2, 10); 
g.addEdge(2, 1, 4); 
g.addEdge(1, 3, 12); 
g.addEdge(2, 4, 14); 
g.addEdge(3, 2, 9); 
g.addEdge(3, 5, 20); 
g.addEdge(4, 3, 7); 
g.addEdge(4, 5, 4); 

# Initialize source and sink 
s = 0
t = 5; 

print("Maximum flow is ",  g.getMaxFlow(s, t));

# The code is contributed by Arushi goel. 

Output

Maximum flow is 23

The code in this article is contributed by Siddharth Lalwani and Utkarsh Trivedi.