Proving Soundness of Armstrong’s Axioms

Last Updated : 17 Sep, 2021

Prerequisite – Armstrong’s Axioms in Functional Dependency in DBMS
Armstrong mentioned that rules 1 through 3 have completeness along with soundness. Armstrong axioms are sound as they do not generate any incorrect Functional Dependencies and it allows us to generate the F⁺ closure.

The proof of Soundness –
Set of functional dependencies that can be derived with logic from a given set of functional dependencies (F_closure) and the set of functional dependencies that can be inferred from Armstrong’s Axioms (F_armstrong) are same. In terms of sets, if we want to show equality, then we mention that one is a proper subset of the other. Hence, we need to prove that,

 F_armstrong is a proper subset of F_closure
    for soundness.

This means that all things derived from F after applying Armstrong’s Axioms are correct functional dependencies and this property is called Soundness.

Consideration for Soundness –
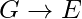$G\to E$ has been derived from F using Armstrong’s Axioms after m number of steps.

In each step we would apply the rules of reflexivity, augmentation and transitivity.
(If we derive from Axioms which are only 3 in number, the repeated application of them would also give similar results.)

Rule of Reflexivity –
This rule states that if E is a proper subset of G, then G implies E (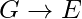 $G\to E$ ). This rule always results in correct Functional Dependencies because it is a trivial functional dependency.

Rule of Augmentation –
This rule states that for 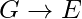$G\to E$ , if we add Z on both sides, then we would get 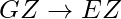$GZ\to EZ$ , which would be a correct functional dependency.
If t_a and t_b have the same corresponding values in G and Z (GZ),
It would mean that they have same corresponding value for G,
which would mean that they have same corresponding value for E, since G implies E,
it would also mean that they correspond to E and Z (EZ).

Rule of Transitivity –
This rule states that if 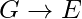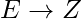$G\to E$ , $E\to Z$ then G determines Z ( $G\to Z$ )
If t_a and t_b have the same corresponding values in G
which would mean that they have same corresponding value for E, since G implies E holds,
it would also mean that they correspond to E, since E implies Z holds.

So, applying these 3 rules will always give rise to correct functional dependencies (even if we apply them m number of times).
Hence proved.