Proving Correctness of Armstrong’s Axioms

Last Updated : 26 Jul, 2021

Prerequisite – Armstrong’s Axioms in Functional Dependency in DBMS
Armstrong mentioned that rules 1 through 3 have completeness along with soundness. Armstrong’s axioms are complete because for a given set of functional dependencies, F, all functional dependencies implied by F⁺ can be derived from F using these rules.

What we need to prove –
The set of functional dependencies that can be derived with logic from a given set of functional dependencies(F_closure) and the set of functional dependencies that can be inferred from Armstrong’s Axioms (F_armstrong) are same. In terms of sets, if we want to show equality, then we write it as, one is a proper subset of the other. Hence, we need to show that,

F_closure is a proper subset of F_armstrong

Correctness means that whatever can be derived from F can also be derived using Armstrong’s Axioms.

F_closure⁺ represents the closure of F. Mathematically we can represent, F_closure⁺ = {A| F_closure⁺ implies A can be derived from F using Armstrong’s Axioms} where, A belongs to Real Numbers.

Claim-1 :
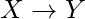$X\to Y$ is derivable from F using Armstrong’s Axioms if and only if Y is a proper subset of F_closure⁺.

To prove ‘if’ part :
Let Y={A₀, A₁, ……, A_m, } where Y is a proper subset of F_closure⁺. F_closure⁺ implies A_j can be derived from F using Armstrong’s Axioms} where, A belongs to 0<j<=m
If we follow union rule then, 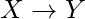$X\to Y$ is derivable from F

To prove the ‘only if’ part :
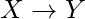$X\to Y$ is derivable from F using Armstrong’s Axioms
by projection rule we know that F_closure⁺ implies A_jwhere, A belongs to 0<j<=m
Thus by the property of F_closure⁺, A_j belongs to F_closure⁺.
This implies that Y is a proper subset of F_closure⁺.

X determines Y follows from F using Armstrong’s Axioms.
We shall try to prove the contrapositive of the above statement.
We would prove that X determines Y cannot be determined from F using Armstrong’s Axioms. In terms of tuple Relations we can say that, There exists an instance r belonging to Real numbers such that, all the functional dependencies of F hold on r. However, X implies Y does not hold.
This mentions that our assumption was wrong and the claim stands correct.
Hence proved that Claim 01 is correct.

Let us consider that r has only 2 rows and is represented by r{F_closure⁺ attributes, other attributes}

Claim-2 :
All FDs of F are satisfied by r. Let us again take the negative of it. Let W implies R belonging to F does not satisfy r, then W is a proper subset of F_closure⁺ and Z is not a proper subset of F_closure⁺.
Let G belongs to Z- F_closure⁺

We get :
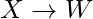$X\to W$ because W is a proper subset of F_closure⁺,
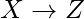$X\to Z$ by rule of transitivity,
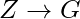$Z\to G$ by rule of reflexivity as G belongs to Z and
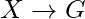$X\to G$ by rule of transitivity.

By definition of closures G must belong to F_closure⁺
We get a contradiction.
We had taken a contradiction which was proven wrong, which means that the statement is true.
Hence proved that Claim 02 is correct.

Claim-3 :
X implies Y is not satisfied by r.
We assume the contradiction again (X does not imply Y). Due to the Structure of r, Y is a proper subset of F_closure⁺ which means that X implies Y can be proved using Armstrong’s Axioms.
Our assumption is proved false hence the claim is correct.
Hence proved that Claim 03 is correct.

These mean that when X does not imply Y, using Armstrong’s Axioms, then F doesn’t logically imply that X implies Y.
We can also say that when X implies Y, using Armstrong’s Axioms (mechanically), then F logically implies that X implies Y as well.
Hence proved that Armstrong’s Axioms are complete.