Prove the identity: (cos (X – Y))/(cosX.cosY) = 1 + tanX.tanY
Last Updated :
12 Dec, 2021
Trigonometry is the relation between the angles and sides of a right-angled triangle. In a right angles triangle, there are 3 angles of which one angle is a right angle (90°) and the other two angles are acute angles and there are 3 sides. The side opposite to the right angle is called Hypotenuse. There are 6 ratios between these sides based on the angle between them and they are called Trigonometric Ratios.
The 6 Trigonometric ratios are:
- Sine (sin)
- Cosine (cos)
- Tangent (tan)
- Cosecant (cosec)
- Secant (sec)
- Cotangent (cot)
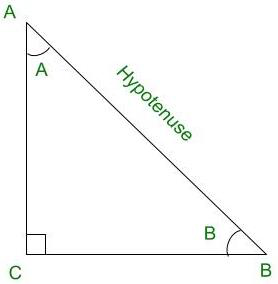
Right Angled Triangle CBA
Sine (sin):
Sine of an angle is defined by the ratio of lengths of sides which is opposite to the angle and the hypotenuse. For the above triangle, sin A = BC/AB
Cosine (cos):
Cosine of an angle is defined by the ratio of lengths of sides which is adjacent to the angle and the hypotenuse. For the above triangle, cos A = AC/AB
Tangent (tan):
Tangent of an angle is defined by the ratio of the length of sides which is opposite to the angle and the side which is adjacent to the angle. For the above triangle, tan A = BC/AC
Cosecant (cosec):
Cosecant of an angle is defined by the ratio of length of the hypotenuse and the side opposite the angle. For the above triangle, cosec A = AB/BC
Secant (sec):
Secant of an angle is defined by the ratio of the length of the hypotenuse and the side and the side adjacent to the angle For the above triangle, sec A = AB/AC
Cotangent (cot):
Cotangent of an angle is defined by the ratio of the length of sides that is adjacent to the angle and the side which is opposite to the angle. For the above triangle, cot A = AC/BC
Prove that: {cos (X – Y)}/{cosX.cosY } = 1 + tanX.tanY

Right Angled Triangle XZY
L.H.S = {cos (X – Y)}/{cosX.cosY}
We know that, cos (A – B) = cosA.cosB + sinA.sinB
⇒ L.H.S = (cosX.cosY + sinX.sinY) / (cosX.cosY)
= (cosX.cosY/cosX.cosY) + (sinX.sinY)/(cosX.cosY)
= 1 + (sinX.sinY)/(cosX.cosY)
Since tanA = sinA/cosA,
⇒ L.H.S = 1 + tanX.tanY ………………..( 1 )
R.H.S = 1 + tanX.tanY ………………..( 2 )
From (1) and (2)
L.H.S = R.H.S
⇒ {cos (X – Y)}/{cosX.cosY} = 1 + tanX.tanY
Hence proved.
Similar Questions
Question 1: Prove the given identity. {cos (X + Y)}/{cosX.cosY } = 1 – tanX.tanY
Proof:
L.H.S = {cos (X + Y)}/{cosX.cosY}
We know that, cos (A + B) = cosA.cosB – sinA.sinB
⇒ L.H.S = (cosX.cosY – sinX.sinY)/(cosX.cosY)
= ( cosX.cosY / cosX.cosY ) – ( sinX.sinY ) / ( cosX.cosY )
= 1 – ( sinX.sinY ) / ( cosX.cosY )
Since tanA = sinA / cosA,
⇒ L.H.S = 1 – tanX.tanY ………………..( 1 )
R.H.S = 1 – tanX.tanY ………………..( 2 )
From ( 1 ) and ( 2 )
L.H.S = R.H.S
⇒ {cos (X + Y)}/{cosX.cosY } = 1 – tanX.tanY
Hence proved.
Question 2: Prove the given identity. {sin (X – Y)}/{cosX.cosY } = tanX – tanY
Proof:
L.H.S = {sin (X – Y)}/{cosX.cosY}
We know that, sin (A – B) = sinA.cosB – cosA.sinB
⇒ L.H.S = (sinX.cosY – cosX.sinY)/(cosX.cosY)
= (sinX.cosY / cosX.cosY) – (cosX.sinY) / (cosX.cosY)
Since tanA = sinA / cosA,
⇒ L.H.S = tanX – tanY ………………..( 1 )
R.H.S = tanX – tanY ………………..( 2 )
From (1) and (2)
L.H.S = R.H.S
⇒ {sin (X – Y)}/{cosX.cosY} = tanX – tanY
Hence proved.
Question 3: Prove the given identity. {sin (X + Y)}/{cosX.cosY} = tanX + tanY
Proof:
L.H.S = {sin (X + Y)}/{cosX.cosY }
We know that, sin (A + B) = sinA.cosB + cosA.sinB
⇒ L.H.S = (sinX.cosY + cosX.sinY) / (cosX.cosY)
= (sinX.cosY / cosX.cosY) + (cosX.sinY) / (cosX.cosY)
Since tanA = sinA / cosA,
⇒ L.H.S = tanX + tanY ………………..( 1 )
R.H.S = tanX + tanY ………………..( 2 )
From (1) and (2)
L.H.S = R.H.S
⇒ {sin (X + Y)}/{cosX.cosY} = tanX + tanY
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...