Prerequisite: Wumpus World in Artificial Intelligence
In this article, we’ll use our understanding to make wumpus world agents that use propositional logic. The first stage is to enable the agent to deduce the state of the world from its percept history to the greatest extent possible. This necessitates the creation of a thorough logical model of the consequences of actions. We also demonstrate how the agent may keep track of the world without having to return to the percept history for each inference. Finally, we demonstrate how the agent may develop plans that are guaranteed to meet its objectives using logical inference.
Wumpus World’s Current State
A logical agent works by deducing what to do given a knowledge base of words about the world. Axioms are the general information about how the universe works combine with percept sentences gleaned from the agent’s experience in a specific reality to form the knowledge base.
Understanding Axioms
We’ll start with the immutable aspects of the Wumpus world and move on to the mutable aspects later. For the time being, we’ll need the following symbols for each ![Rendered by QuickLaTeX.com [x, y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9e09227407756c8ab5ddcb7093d5ab_l3.png) coordinate:
coordinate:
- If there is a pit in
![Rendered by QuickLaTeX.com [x, y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9e09227407756c8ab5ddcb7093d5ab_l3.png) ,
, 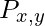 is true.
is true. - If there is a Wumpus in
![Rendered by QuickLaTeX.com [x, y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9e09227407756c8ab5ddcb7093d5ab_l3.png) , whether dead or living,
, whether dead or living, 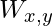 is true.
is true. - If the agent perceives a breeze in
![Rendered by QuickLaTeX.com [x, y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9e09227407756c8ab5ddcb7093d5ab_l3.png) ,
, 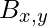 is true.
is true. - If the agent detects a smell in
![Rendered by QuickLaTeX.com [x, y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9e09227407756c8ab5ddcb7093d5ab_l3.png) ,
, 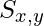 is true.
is true.
The sentences we write will be adequate to infer 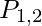 (there is no pit in
(there is no pit in ![Rendered by QuickLaTeX.com [1,2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-23652c724be867ed1a7891412f44ccf1_l3.png) labelled). Each sentence is labeled
labelled). Each sentence is labeled 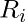 so that we can refer to it:
so that we can refer to it:
- In
![Rendered by QuickLaTeX.com [1, 1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d648a975e23b93f98eee12479ae68ab_l3.png) , there is no pit:
, there is no pit: 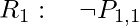
- A square is breezy if and only if one of its neighbours has a pit. This must be stated for each square; for the time being, we will only add the relevant squares:
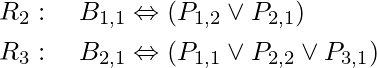
- In all Wumpus universes, the previous sentences are correct. The breeze percepts for the first two squares visited in the specific environment the agent is in are now included.
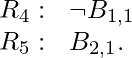
The agent is aware that there are no pits 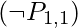 or Wumpus
or Wumpus 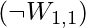 in the starting square. It also understands that a square is windy if and only if a surrounding square has a pit, and that a square is stinky if and only if a neighbouring square has a Wumpus. As a result, we include a huge number of sentences of the following type:
in the starting square. It also understands that a square is windy if and only if a surrounding square has a pit, and that a square is stinky if and only if a neighbouring square has a Wumpus. As a result, we include a huge number of sentences of the following type:
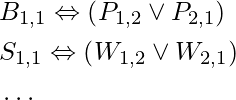
The agent is also aware that there is only one wumpus on the planet. This is split into two sections. First and foremost, we must state that there is at least one wumpus:

Then we must conclude that there is only one wumpus. We add a statement to each pair of places stating that at least one of them must be wumpus-free:
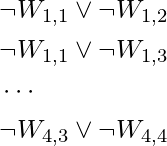
So far, everything has gone well. Let’s look at the agent’s perceptions now. If there is now a stink, the knowledge base would benefit from the addition of the proposition 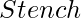 . However, if there was no stench at the prior time step, then
. However, if there was no stench at the prior time step, then 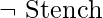 would have already been stated, and the new assertion would simply be a contradiction. When we grasp that a percept simply states anything about the current time, the dilemma is solved. As a result, if the time step (as provided to MAKE-PERCEPT-SENTENCE is 4, we add Stench4 to the knowledge base instead of Stench, neatly avoiding any possible conflict with Stench3. The same may be said for the percepts of wind, bump, sparkle, and scream.
would have already been stated, and the new assertion would simply be a contradiction. When we grasp that a percept simply states anything about the current time, the dilemma is solved. As a result, if the time step (as provided to MAKE-PERCEPT-SENTENCE is 4, we add Stench4 to the knowledge base instead of Stench, neatly avoiding any possible conflict with Stench3. The same may be said for the percepts of wind, bump, sparkle, and scream.
Associating propositions with time steps is a concept that may be applied to any feature of the universe that changes through time. 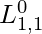 —the agent is in square
—the agent is in square ![Rendered by QuickLaTeX.com [1,1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f75e4d0f32593ed98cb5a24344b065e1_l3.png) at time 0—as well as FacingEast, HaveArrow, and WumpusAlive — are all included in the initial knowledge base. We use the term fluent (from the Latin fluent, which means “flowing”) to describe a changing element of the environment. “Fluent” is a synonym for “state variable”. Atemporal variables are symbols that are related to permanent elements of the world and do not require a time superscript.
at time 0—as well as FacingEast, HaveArrow, and WumpusAlive — are all included in the initial knowledge base. We use the term fluent (from the Latin fluent, which means “flowing”) to describe a changing element of the environment. “Fluent” is a synonym for “state variable”. Atemporal variables are symbols that are related to permanent elements of the world and do not require a time superscript.
Through the location fluent, we can directly link stink and wind percepts to the attributes of the squares where they are encountered.
We assert
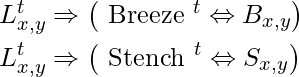
for every time step t and any square ![Rendered by QuickLaTeX.com [x,y]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1980dec6d7288c3bddea22233b4199c8_l3.png) .
.
Of course, axioms are required to allow the agent to keep track of fluents like  . These fluents change as a result of the agent’s activities, thus we need to write down the wumpus world’s transition model as a series of logical statements.
. These fluents change as a result of the agent’s activities, thus we need to write down the wumpus world’s transition model as a series of logical statements.
For starters, we’ll need proposition symbols for action occurrences. These symbols, like percepts, are indexed by time; for example, Forward 0 indicates that the agent performs the Forward action at time 0. The percept for a given time step occurs first, followed by the action for that time step, and then a transition to the next time step, according to the convention.
We can attempt defining effect axioms that explain the outcome of an action at the following time step to describe how the world changes. If the agent is at ![Rendered by QuickLaTeX.com [1,1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2fef54e96e69cea8355c3cfe10818354_l3.png) facing east at time 0 and goes Forward, the consequence is that the agent is now in square
facing east at time 0 and goes Forward, the consequence is that the agent is now in square ![Rendered by QuickLaTeX.com [2, 1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-579238e320e0ac2590224901114559c0_l3.png) and no longer in
and no longer in ![Rendered by QuickLaTeX.com [1, 1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-caf4b57856e79dad798bfceedf0ad3a6_l3.png) :
:
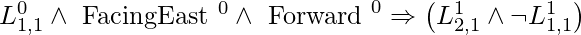
Each potential time step, each of the 16 squares, and each of the four orientations would require a separate statement. For the other actions, we’d need comparable sentences: grab, shoot, climb, turnLeft, and turnRight.
Assume the agent decides to travel Forward at time 0 and records this information in its knowledge base. The agent can now derive that it is in [2, 1] using the effect axiom in the above equation and the initial statements about the state at time 0. \operatorname{ASK}\left(K B, L_{2,1}^{1}\right)=\operatorname{true}, in other words. So far, everything has gone well. Unfortunately, the news isn’t so good elsewhere: if we \operatorname{ASK}\left(K B, \text { HaveArrow }^{1}\right), the result is false, which means the agent can’t show it still has the arrow or that it doesn’t! Because the effect axiom fails to explain what remains unchanged as a result of an action, the knowledge has been lost. The frame problem arises from the need to do so. Adding frame axioms explicitly expressing all the propositions that remain the same could be one answer to the frame problem. For each time t, we would have
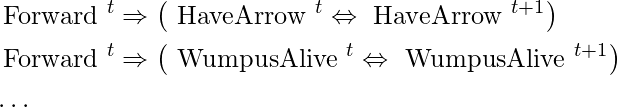
Despite the fact that the agent now knows it still retains the arrow after going ahead and that the wumpus hasn’t been killed or resurrected, the proliferation of frame axioms appears to be incredibly inefficient. The set of frame axioms in a universe with m distinct actions and n fluents will be of size O. (mn). The representational frame problem is a term used to describe this particular form of the frame problem. The problem has historically been a significant one for AI researchers; we go over it in more detail in the chapter’s notes.
The representational frame problem is significant because, to put it kindly, the real world has a large number of fluents. Fortunately for us, each action normally affects only a small number of those fluents — the world demonstrates localization. To solve the representational frame problem, the transition model must be defined using a set of axioms of size 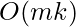 rather than size
rather than size 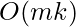 . There’s also the inferential frame problem, which involves projecting the results of a t-step action plan ahead in time
. There’s also the inferential frame problem, which involves projecting the results of a t-step action plan ahead in time 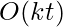 rather than
rather than 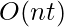 .
.
The difficulty can be solved by shifting one’s attention from writing axioms about actions to writing axioms about fluents. As a result, we will have an axiom for each fluent 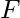 that describes the truth value of
that describes the truth value of 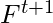 in terms of fluents (including
in terms of fluents (including 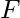 itself) at time t and possible actions at time t. Now, the truth value of
itself) at time t and possible actions at time t. Now, the truth value of 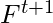 can be set in one of two ways: either the action at time t causes
can be set in one of two ways: either the action at time t causes 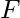 to be true at time
to be true at time 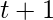 , or F was already true at time t and the activity at time t has no effect on it. A successor-state axiom is a type of axiom that has the following schema:
, or F was already true at time t and the activity at time t has no effect on it. A successor-state axiom is a type of axiom that has the following schema:
F^{t+1} \Leftrightarrow \text { ActionCausesF }^{t} \vee\left(F^{t} \wedge \neg \text { ActionCausesNotF }^{t}\right)
The HaveArrow axiom is one of the most basic successor-state axioms. Because there is no action for reloading, the 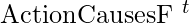 section is removed, leaving us with
section is removed, leaving us with
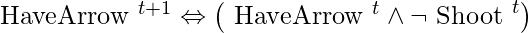
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...