Properties of Determinants are the properties that are required to solve various problems in Matrices. There are various properties of the determinant that are based on the elements, rows, and columns of the determinant. These properties help us to easily find the value of the determinant. Suppose we have a matrix M = [aij] then the determinant of the matrix is denoted as, |M| or det M. There are various properties of the determinant of a matrix, and some of the important ones are, Reflection Property, Switching Property, Scalar Multiple Properties, Sum Property, Invariance Property, Factor Property, Triangle Property, Co-Factor Matrix Property, All-Zero Property, and Proportionality or Repetition Property,
In this article, we will learn about all the properties of the determinant with examples and others in detail.
What are Determinants?
Determinant of a matrix is the value obtained by solving any square matrix in a particular order. Suppose we have a square matrix A of order 2, i.e.
A = 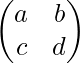
Then determinant of A is defined as,
|A| = 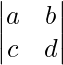
|A| = ad – bc
This is the value of the determinant of matrix A, similarly the determinant of all square matrices are calculated.
What are Properties of Determinants?
There are various rules and properties that are used to easily find the value of the determinant which are called the Properties of Determinant. There are various properties of the determinant and some of the important one are,
- Triangle Property
- Determinant of Cofactor Matrix
- Factor Property
- Property of Invariance
- Scalar Multiple Property
- Reflection Property
- Switching Property
- Repetition Property
- All Zero Property
- Sum Property
Now let’s learn about them in detail.
Properties of Determinant of a Matrix
The various properties of determinants of a Matrix are discussed in detail below:
Triangle Property
This property of the determinant states that if the elements above or below, the main diagonal then the value of the determinant is equal to the product of the diagonal elements.
For any square matrix A such that,
A = 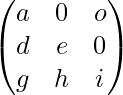
|A| = 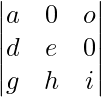
Then according to Traingle Property of Determinant
|A| = a.e.i
Determinant of Cofactor Matrix
For any matrix square matrix A of order 2,
A = 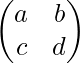
Then determinant of A is defined as,
|A| = 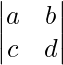
Now suppose the cofactor matrix is, C then the detrminant of cofactor matrix is,
|C| = 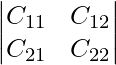
In the above matrix Cij denotes the cofacts of the respective elements of matrix A.
Factor Property
For any square matrix A of variable ‘x’ if on putting x = a the value of determinant is zero then, (x – a) is a factor of the determinant.
Property of Invariance
Suppose we have a square matrix A of order 3
A = 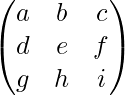
Then adding a scalar multiple of any row or column with the any row or column does not changes the value of determinant, i.e.
Ri → Ri + (q)Rj
OR
Ci → Ci + (q)Cj
where, q represent the scalar constant, then the value of the determinant of the new matrix form does not changes.
|A| = 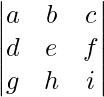
|B| = 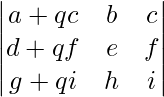
Then the determinant of matrix A and matrix B are equal, i.e.
|A| = |B|
Scalar Multiple Property
If any row or column of a determinant, is multiplied by any scalar value, that is a non-zero constant, the entire determinant gets multiplied by the same scalar, that is, if any row or column is multiplied by constant k, the determinant value gets multiplied by k. Constants may be any real number.
Example:
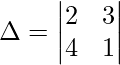
Δ = 2.1 – 4.3
Δ = 2 – 12 = -10
Now, multiplying by k = 1/2, in first row,
Δ’ = 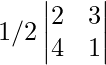
Δ’ = 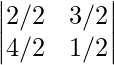
Δ’ = 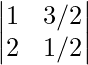
Δ’ = 1(1) – 4(3/2) = -5
Therefore,
(Δ’) = 1/2 (Δ)
det(Δ’) = k det(Δ)
Transpose of Determinant (Reflection Property)
Transpose refers to the operations of interchanging rows and columns of the determinant. The rows become columns and columns become rows in order. It is denoted by |AT|, for any determinant |A|.
The property says determinant remains unchanged on its transpose, that is, |AT| = |A|.
Example:
|A| = 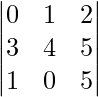
|A| = -12
|AT| = 
|AT| = -12
det(A) = det(AT)
Switching Property
If we interchange any two rows/columns of the determinant, the magnitude (i.e. the sign) changes, but the determinant value remains the same.
Now,
Value of Determinant = (-1)number of exchanges
Example: Apply switching property in,
Δ = 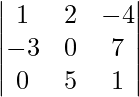
If we interchange C1 and C3, denoted by C1 ↔ C3
Δ’ = 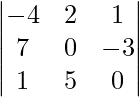
det (Δ) = -det(Δ’)
If we again interchange R1 and R2, denoted by R1 ↔ R2
Δ” = 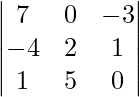
det(Δ”) = -det(Δ’) = det (Δ)
Repetition Property
If any pair of rows or columns of a determinant are exactly identical or proportion by same amount, then the determinant is zero.
All Zero Property
If all elements of any column or row are zero, then the determinant is zero
For any matrix,
A = 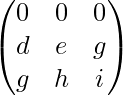
⇒ |A| = 0
Sum Property
If all the elements of a row or columns in a determinant are expressed as a summation of two or more numbers, then the determinant can be broken down as a sum of corresponding smaller determinants.
We have, 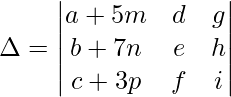
Then, 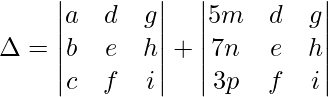
Also, Check
Properties of Determinants Examples
Example 1: Verify det(Δ’) = k det(Δ) in,
Δ = 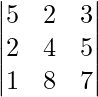
k = 3/2
Solution:
Δ = 
det(Δ) = 5[(4×7) – (8×5)] – 2[(2×7) – (5×1)] + 3[(2×8) – (4×1)]
det(Δ) = -60 – 18 + 36
det(Δ) = -42
Now, on multiplying by k = 3/2, first column,
Δ’ = 
Δ’ = 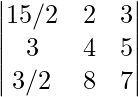
det (Δ’) = -63
Therefore,
det(Δ’) = 3/2 det(Δ)
⇒ det(Δ’) = k det(Δ)
Example 2: Find the Determinant of
[A] = 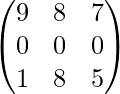
Solution:
|A| = 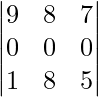
det(Δ) = 0 (since R2 ⇢0)
Example 3: Find the Determinant of
[A] = 
Solution:
|A| = 
det(Δ) = 2 × 1 × 8 × 9
det(Δ) = 144
FAQs on Properties of Determinant
1. What are Properties of Determinant?
Properties of the determinant are various properties that are used to easily find the value of determinant of any square matrix.
2. What is Reflection Property of Determinants?
Reflaction properties of determinant is the properties if we interchage any two rows OR any two columns then the value of determinant does not changes only the sign of the determinant changes.
3. What happens to Determinant if 2 Rows or Columns of the Determinant are interchanged?
The value of the determinant changes its sign when 2 rows or columns are interchanged.
4. What is All-Zero Property of Determinant?
All-Zero Property of Determinant states that, if in any row or column all the elements are zero then the value of dertminat is zero.
5. What is Sum Property of Determinant?
Sum Property of Determinant stares that, if any row or column all the elements are sum of two numbers then the derteminant can be slpit into two determinant.
6. What is Triangle Property of Determinant?
Triangle property of determinant states that, if all the elements of below and above the main diagonal are zero. Then the value of the determinant is the product of all the elements of main diagonals.
7. What we have to study in Properties of Determinant Class 12?
We have to study Triangle Property, sum property, switch property, invariance property, scalar multiple property, transpose property, repetition property and all zero property in Properties of Determinant of Class 12.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...