Proof of De-Morgan’s laws in boolean algebra

Statements :

1.

2.

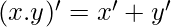
Proof:

Here we can see that we need to prove that the two propositions are complement to each other. We know that

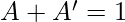
and

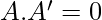
which are annihilation laws. Thus if we prove these conditions for the above statements of the laws then we shall prove that they are complement of each other.

For statement 1:

We need to prove that:

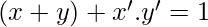
and

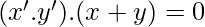
Case 1.

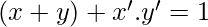
[Tex]LHS: (x+y)+x’.y’ =(x+y).(x+x’)+x’.y’ [/Tex]

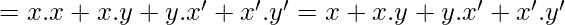
{Using distributive property}

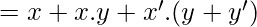
[Tex]=x+x.y+x’=x+x’+x.y [/Tex]

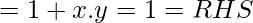
Hence proved.

Case 2.

[Tex]LHS: (x’.y’).(x+y)=x.(x’y’)+y.(x’.y’) [/Tex]

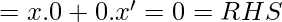
Hence proved.

For statement 2:

We need to prove that:

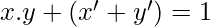
and

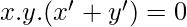
Case 1.

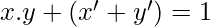
[Tex] LHS: x.y+(x’+y’)=(x+x’+y’).(y+x’+y’) [/Tex]

{We know that A+BC=(A+B).(A+C)}

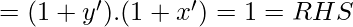
Hence proved.

Case 2.

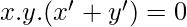
[Tex]LHS: (x.y).(x’+y’)=x.x’.y+x.y.y’ [/Tex]

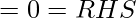
Hence Proved. This proves the De-Morgan’s theorems using identities of Boolean Algebra.

Proof of De-Morgan’s law of boolean algebra using Truth Table:

1) (x+y)’= x’. y’

x	y	x+y	(x+y)’	x’	y’	x’. y’
0	0	0	1	1	1	1
0	1	1	0	1	0	0
1	0	1	0	0	1	0
1	1	1	0	0	0	0

Hence the first De-morgan law of boolean algebra is proved (x+y)’= x’. y’

2) (x.y)’=x’+y’

x	y	x.y	(x.y)’	x’	y’	x’+y’
0	0	0	1	1	1	1
0	1	0	1	1	0	1
1	0	0	1	0	1	1
1	1	1	0	0	0	0

Hence the second De-morgan law of boolean algebra is proved (x.y)’=x’+y’