Program to solve the Alligation Problem

Write a program to find the ratio in which a shopkeeper will mix two types of rice worth Rs. 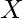kg and Rs. 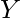kg, so that the average cost of the mixture is Rs. 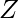kg.

Examples: 

Input: X = 50, Y = 70, Z = 65
Output: Ratio = 1:3

Input: X = 1000, Y = 2000, Z = 1400
Output: Ratio = 3:2

According to Alligation rule, the ratio of the weights of two items mixed will be inversely proportional to the deviation of attributes of these two items from the average attribute of the resultant mixture.

w1 / w2 = (d - m) / (m - c)

Below program illustrate the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

// Function to find the ratio of two mixtures
void alligation(float x, float y, float m)
{
    // Find the cheaper among x and y
    float c = (x <= y) ? x : y;
    // Find the dearer among x and y
    float d = (x >= y) ? x : y;

    // Find ratio r1:r2
    int r1 = d - m;
    int r2 = m - c;

    // Convert the ration into simpler form
    int gcd = __gcd(r1, r2);

    cout << r1 / gcd << ":" << r2 / gcd;
}

// Driver code
int main()
{
    float x, y, z;
    x = 50;
    y = 70;
    z = 65;

    alligation(x, y, z);

    return 0;
}

Java

// Java implementation of the
// above approach.
import java.util.*;

class solution
{

static float __gcd(float a, float b)
{
    float dividend,divisor;

    // a is greater or equal to b
    if(a>=b)
    dividend = a;
    else
    dividend = b;

    // b is greater or equal to a
    if(a<=b)
    divisor = a;
    else
    divisor = b;

while(divisor>0)
{
float remainder = dividend % divisor;
dividend = divisor;
divisor = remainder;

}
return dividend;
}
// Function to find the ratio of two mixtures
static void alligation(float x, float y, float m)
{
    // Find the cheaper among x and y
    float c;
    if (x <= y)
    c = x;
    else
    c = y;
    // Find the dearer among x and y
    float d ;
    if (x >= y)
    d = x;
    else
    d = y;

    // Find ratio r1:r2
    float r1 = d - m;
    float r2 = m - c;

    // Convert the ration into simpler form
    float gcd = __gcd(r1, r2);

    System.out.println((int)(r1 / gcd)+":"+(int)(r2 / gcd));
}

// Driver code
public static void main(String args[])
{
    float x, y, z;
    x = 50;
    y = 70;
    z = 65;

    alligation(x, y, z);
}
}

// This code is contributed by
// Shashank_sharma

Python3

# Python 3 implementation of the
# above approach.
from math import gcd

# Function to find the ratio
# of two mixtures
def alligation(x, y, m):

    # Find the cheaper among x and y
    if (x <= y):
        c = x
    else:
        c = y

    # Find the dearer among x and y
    if (x >= y):
        d = x
    else:
        d = y

    # Find ratio r1:r2
    r1 = d - m
    r2 = m - c

    # Convert the ration into simpler form
    __gcd = gcd(r1, r2)

    print(r1 // __gcd, ":", r2 // __gcd)

# Driver code
if __name__ == '__main__':
    x = 50
    y = 70
    z = 65

    alligation(x, y, z)

# This code is contributed by
# Surendra_Gangwar

C#

// C# implementation of the
// above approach.
using System;

class GFG
{
    // Recursive function to return
    // gcd of a and b
    static int __gcd(int a, int b)
    {
        // Everything divides 0
        if (a == 0)
            return b;
        if (b == 0)
            return a;

        // base case
        if (a == b)
            return a;

        // a is greater
        if (a > b)
            return __gcd(a - b, b);
        return __gcd(a, b - a);
    }

    // Function to find the ratio of
    // two mixtures
    static void alligation(float x,
                           float y, float m)
    {
        // Find the cheaper among x and y
        float c = (x <= y) ? x : y;

        // Find the dearer among x and y
        float d = (x >= y) ? x : y;

        // Find ratio r1:r2
        int r1 = (int)(d - m);
        int r2 = (int)(m - c);

        // Convert the ration into
        // simpler form
        int gcd = __gcd(r1, r2);

        Console.Write(r1 / gcd + ":" +
                      r2 / gcd);
    }

    // Driver code
    public static void Main()
    {
        float x, y, z;
        x = 50;
        y = 70;
        z = 65;

        alligation(x, y, z);
    }
}

// This code is contributed
// by Akanksha Rai

PHP

<?php
// PHP implementation of the
// above approach.
function __gcd($a, $b)
{
    $dividend; $divisor;

    // a is greater or equal to b
    if($a >= $b)
        $dividend = $a;
    else
        $dividend = $b;

    // b is greater or equal to a
    if($a <= $b)
        $divisor = $a;
    else
        $divisor = $b;

    while($divisor > 0)
    {
        $remainder = $dividend % $divisor;
        $dividend = $divisor;
        $divisor = $remainder;
    }
    return $dividend;
}

// Function to find the ratio of
// two mixtures
function alligation($x, $y, $m)
{
    // Find the cheaper among x and y
    if ($x <= $y)
        $c = $x;
    else
        $c = $y;

    // Find the dearer among x and y
    if ($x >= $y)
        $d = $x;
    else
        $d = $y;

    // Find ratio r1:r2
    $r1 = $d - $m;
    $r2 = $m - $c;

    // Convert the ration into
    // simpler form
    $gcd = __gcd($r1, $r2);

    echo (int)($r1 / $gcd) . ":" .
         (int)($r2 / $gcd);
}

// Driver code
$x = 50;
$y = 70;
$z = 65;

alligation($x, $y, $z);

// This code is contributed by
// Mukul Singh
?>

Javascript

<script>
    // Javascript implementation of the above approach.

    // Recursive function to return
    // gcd of a and b
    function __gcd(a, b)
    {
        // Everything divides 0
        if (a == 0)
            return b;
        if (b == 0)
            return a;

        // base case
        if (a == b)
            return a;

        // a is greater
        if (a > b)
            return __gcd(a - b, b);
        return __gcd(a, b - a);
    }

    // Function to find the ratio of
    // two mixtures
    function alligation(x, y, m)
    {
        // Find the cheaper among x and y
        let c = (x <= y) ? x : y;

        // Find the dearer among x and y
        let d = (x >= y) ? x : y;

        // Find ratio r1:r2
        let r1 = (d - m);
        let r2 = (m - c);

        // Convert the ration into
        // simpler form
        let gcd = __gcd(r1, r2);

        document.write(parseInt(r1 / gcd, 10) + ":" + parseInt(r2 / gcd, 10));
    }

    let x, y, z;
    x = 50;
    y = 70;
    z = 65;

    alligation(x, y, z);

// This code is contributed by mukesh07.
</script>

Output:

1:3

Time Complexity: O(log(min(x,y)), gcd function takes logarithmic time complexity.
Auxiliary Space: O(1) as constant space is being used.