Program to find weighted median of a given array
Last Updated :
21 Jun, 2021
Given two arrays arr[] of N integers and W[] of N weights where W[i] is the weight for the element arr[i]. The task is to find the weighted median of the given array.
Note: The sum of the weight of all elements will always be 1.
Let the array arr[] be arranged in increasing order with their corresponding weights.
If N is odd, then there is only one weighted median say arr[k] which satisfies the below property:
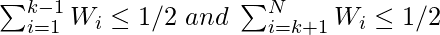
If N is even, then there are two weighted medians, i.e., lower and upper weighted median.
The lower weighted median for element arr[k] which satisfies the following:
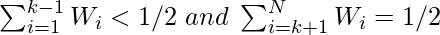
The upper weighted median for element arr[k] which satisfies the following:
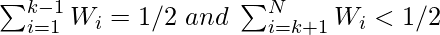
Examples:
Input: arr={5, 1, 3, 2, 4}, W=[0.25, 0.15, 0.2, 0.1, 0.3]
Output: The weighted median is element 4
Explanation:
Here the number of element is odd, so there is only one weighted median because at K = 3 the above condition is satisfied.
The cumulative weights on each side of element 4 is 0.45 and 0.25.
Input: arr=[4, 1, 3, 2], W=[0.25, 0.49, 0.25, 0.01]
Output:
The lower weighted median is element 2
The upper weighted median is element 3
Explanation:
Here there are an even number of elements, so there are two weighted medians.
Lower weighted median is at K = 2 because at K = 2 the above condition is satisfied with cumulative weight on each side of element 2 is 0.49 and 0.5.
Upper weighted median is at K = 3 because at K = 3 the above condition is satisfied with cumulative weight on each side of element 3 is 0.5 and 0.25.
Approach: Follow the steps below to solve the given problem:
- Now to find the median of the array arr[] in increasing order with their respective order of weight shouldn’t be changed.
- So, create a set of pairs where the first element of the pair will be arr[i] and the second element of the pair will be its corresponding weights W[i].
- Then sort the set of Pairs according to the arr[] values.
- If the number of pairs is odd, then find the weighted median as:
- Traverse over the set of pairs and compute sum by adding weights.
- When the sum becomes greater than 0.5 print the arr[i] value of that Pair.
- But, if the number of pairs is even, then find both lower and upper weighted medians:
- For the lower median traverse over the set pairs from the left and compute sum by adding weights.
- When the sum becomes greater than or equal to 0.5 print the arr[i] value of that Pair.
- For the upper median traverse over the set pairs from the right and compute sum by adding weights.
- When the sum becomes greater than or equal to 0.5 print the arr[i] value of that Pair.
Below is the implementation of the above approach:
C++14
#include <bits/stdc++.h>
using namespace std;
void weightedMedian(vector<int> arr,
vector<float> W)
{
vector<pair<int, float>> pr;
for(int index = 0;
index < arr.size();
index++)
pr.push_back({arr[index],
W[index]});
sort(pr.begin(), pr.end());
if (arr.size() % 2 != 0)
{
float sums = 0;
for(auto element : pr)
{
sums += element.second;
if (sums > 0.5)
cout << "The Weighted Median is element "
<< element.first << endl;
}
}
else
{
float sums = 0;
for(auto element : pr)
{
sums += element.second;
if (sums >= 0.5)
{
cout << "Lower Weighted Median is element "
<< element.first << endl;
break;
}
}
sums = 0;
for(int index = pr.size() - 1;
index >= 0;
index--)
{
int element = pr[index].first;
float weight = pr[index].second;
sums += weight;
if (sums >= 0.5)
{
cout << "Upper Weighted Median is element "
<< element;
break;
}
}
}
}
int main()
{
vector<int> arr = { 4, 1, 3, 2 };
vector<float> W = { 0.25, 0.49, 0.25, 0.01 };
weightedMedian(arr, W);
}
|
Java
import java.util.*;
class GFG{
static class Pair implements Comparable<Pair>
{
int first;
double second;
Pair(int f, double s)
{
first = f;
second = s;
}
@Override
public int compareTo(Pair o)
{
if(this.second > o.second)
return 1;
else if(this.second == o.second)
return 0;
return -1;
}
}
static void weightedMedian(Vector<Integer> arr,
Vector<Double> W)
{
Vector<Pair> pr = new Vector<>();
for(int index = 0;
index < arr.size();
index++)
pr.add(new Pair(arr.get(index),
W.get(index)));
Collections.sort(pr);
if (arr.size() % 2 != 0)
{
float sums = 0;
for(Pair element : pr)
{
sums += element.second;
if (sums > 0.5)
System.out.print(
"The Weighted Median is element " +
element.first + "\n");
}
}
else
{
double sums = 0;
for(Pair element : pr)
{
sums += element.second;
if (sums <= 0.5)
{
System.out.print(
"Lower Weighted Median is element " +
element.first + "\n");
break;
}
}
sums = 0;
for(int index = pr.size() - 1;
index >= 0; index--)
{
int element = pr.get(index).first;
double weight = pr.get(index).second;
sums += weight;
if (sums >= 0.5)
{
System.out.print(
"Upper Weighted Median is element " +
element);
break;
}
}
}
}
public static void main(String[] args)
{
Vector<Integer> arr = new Vector<>();
arr.add(4);
arr.add(1);
arr.add(3);
arr.add(2);
Vector<Double> W = new Vector<>();
W.add(0.25);
W.add(0.49);
W.add(0.25);
W.add(0.01);
weightedMedian(arr, W);
}
}
|
Python3
def weightedMedian(arr, W):
pairs = []
for index in range(len(arr)):
pairs.append([arr[index], W[index]])
pairs.sort(key = lambda p: p[0])
if len(arr) % 2 != 0:
sums = 0
for element, weight in pairs:
sums += weight
if sums > 0.5:
print("The Weighted Median", end = ' ')
print("is element {}".format(element))
else:
sums = 0
for element, weight in pairs:
sums += weight
if sums >= 0.5:
print("Lower Weighted Median", end = ' ')
print("is element {}".format(element))
break
sums = 0
for index in range(len(pairs)-1, -1, -1):
element = pairs[index][0]
weight = pairs[index][1]
sums += weight
if sums >= 0.5:
print("Upper Weighted Median", end = ' ')
print("is element {}".format(element))
break
if __name__ == "__main__":
arr = [4, 1, 3, 2]
W = [0.25, 0.49, 0.25, 0.01]
weightedMedian(arr, W)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static void weightedMedian(int[] arr,
float[] W)
{
List<Tuple<int,
float>> pr = new List<Tuple<int,
float>>();
for(int index = 0; index < arr.Length; index++)
pr.Add(new Tuple<int, float>(arr[index], W[index]));
pr.Sort();
if (arr.Length % 2 != 0)
{
float sums = 0;
foreach(Tuple<int, float> element in pr)
{
sums += element.Item2;
if (sums > 0.5)
Console.WriteLine("The Weighted Median " +
"is element " + element.Item1);
}
}
else
{
float sums = 0;
foreach(Tuple<int, float> element in pr)
{
sums += element.Item2;
if (sums >= 0.5)
{
Console.WriteLine("Lower Weighted Median " +
"is element " + element.Item1);
break;
}
}
sums = 0;
for(int index = pr.Count - 1; index >= 0; index--)
{
int element = pr[index].Item1;
float weight = pr[index].Item2;
sums += weight;
if (sums >= 0.5)
{
Console.Write("Upper Weighted Median " +
"is element " + element);
break;
}
}
}
}
static void Main()
{
int[] arr = { 4, 1, 3, 2 };
float[] W = { 0.25f, 0.49f, 0.25f, 0.01f };
weightedMedian(arr, W);
}
}
|
Javascript
<script>
function weightedMedian(arr,W)
{
let pr = [];
for(let index = 0;
index < arr.length;
index++)
pr.push([arr[index],
W[index]]);
(pr).sort(function(a,b){return a[1]-b[1];});
if (arr.length % 2 != 0)
{
let sums = 0;
for(let element=0;element< pr.length;element++)
{
sums += pr[element][1];
if (sums > 0.5)
document.write(
"The Weighted Median is element " +
pr[element][0] + "<br>");
}
}
else
{
let sums = 0;
for(let element=0;element< pr.length;element++)
{
sums += pr[element][1];
if (sums <= 0.5)
{
document.write(
"Lower Weighted Median is element " +
pr[element][0] + "<br>");
break;
}
}
sums = 0;
for(let index = pr.length - 1;
index >= 0; index--)
{
let element = pr[index][0];
let weight = pr[index][1];
sums += weight;
if (sums >= 0.5)
{
document.write(
"Upper Weighted Median is element " +
element);
break;
}
}
}
}
let arr = [];
arr.push(4);
arr.push(1);
arr.push(3);
arr.push(2);
let W = [];
W.push(0.25);
W.push(0.49);
W.push(0.25);
W.push(0.01);
weightedMedian(arr, W);
</script>
|
Output: Lower Weighted Median is element 2
Upper Weighted Median is element 3
Time Complexity: O(N log N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...