- Case 1: when x ends with 1
For finding the last two digit of a number, when the number ends with 1 then we have to do following steps shown as in the figure.
Example: 21^48

So, Last two digit of 21^48 is 81.
Example: 31^35
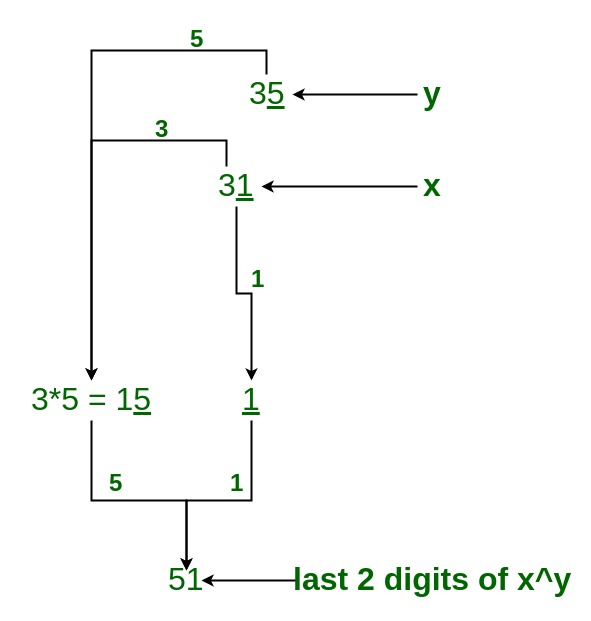
So, Last two digit of 31^35 is 51.
- Case 2: when x ends with 3, 7, 9
For finding the last two digit of a number, when the number ends with 3, 7, 9 then we have to apply cyclicity concept to convert the last digit as a 1.
cyclicity of 3:
3^1 = 3
3^2 = 9
3^3 = 7
3^4 = 1
cyclicity of 7:
7^1 = 7
7^2 = 9
7^3 = 3
7^4 = 1
cyclicity of 9:
9^1 = 9
9^2 = 1
Example1: 23^34
Solution:
- Last digit of 23^34 is 3 so, we use cyclicity of 3 .
- 3^4 gives 1 so, we take 23^4
- ((23)^4)^8 * (23)^2
- last two digit of (23)^4) is 41, so we take (41)^8 and solve according to the given diagram.

- So last digit of (41)^8 is 21 .
- solve (23)^2, the last digit of (23)^2 is 29.
- Now multiply last digit of (41)^8 i.e 21 with the last digit of (23)^2 i.e 29
- i.e 21 * 29 = 609
- So, Last two non zero digit of 23^34 is 09.
Example2: 37^45
Solution:
- Last digit of 37^45 is 7 so, we use cyclicity of 7 .
- 7^4 gives 1 so, we take 37^4
- ((37)^4)^11 * (37)^1
- last two digit of (37)^4) is 61, so we take (61)^11 and solve according to the diagram.

- So last digit of (61)^11 is 61 .
- solve (37)^1, the last digit of (37)^1 is 37.
- Now multiply last digit of (61)^11 i.e 61 with the last digit of (37)^1 i.e 37
- i.e 61 * 37 = 2257
- So, Last two non zero digit of 37^45 is 57.
Example3: 59^22
Solution:
- Last digit of 59^22 is 9 so, we use cyclicity of 9 .
- 9^2 gives 1 so, we take 59^2
- ((59)^2)^11
- last two digit of (59)^2 is 81, so we take (81)^11 and solve according to the diagram.
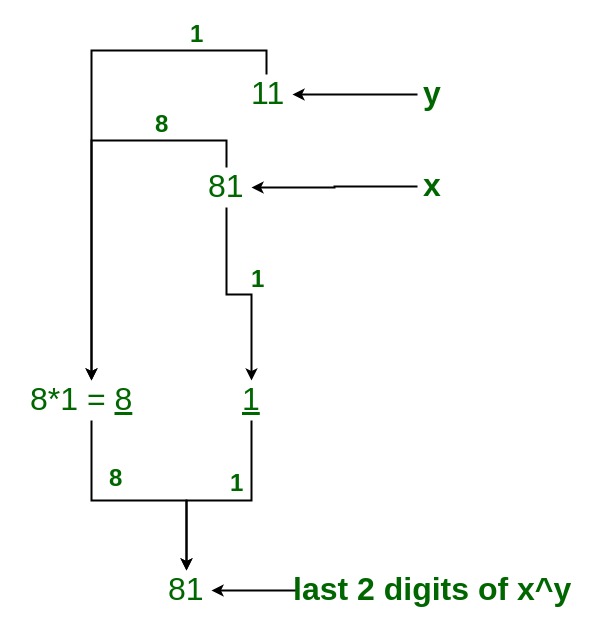
- So last digit of (81)^11 is 81 .
- So, Last two non zero digit of 59^22 is 81.
- Case 3: when x ends with 2, 4, 6, 8
For finding the last digit of a number ends with 2, 4, 6, 8; We use number 76 which is a type of magic number because its square, cube and etc contain last 2 digit numbers as itself i.e 76.
Take an example :
square of 76 = 5776, its last two digit =76
cube of 76 = 438976, its last two digit=76
So we take two cases:
- if (2^10)^even power then it always return 76 .
- if (2^10)^odd power then it always return 24 .
Steps for finding last two digits
- Firstly, convert given number in to these formats if (2^10)^power.
Here power will be odd or even according to the question.
- Now, check power will be odd or even.
- if power is odd then its value will be 24.
- if power is even then its value will be 76.
Examples
Example1: Find last 2 digit of 2^453.
Solution:
- Step 1:- conversion
2^453 = (2^10)^45 * 2^3
- Step 2:- odd power so we take 24
= 24 * 8
= 192
So, Last two non zero digits of 2^453 are 92.
Example2: Find last 2 digits of 4^972.
Solution:
- step 1:- conversion
4^972 = (2^2)^972
= 2^1944
= (2^10)^194 * 2^4
- step 2:- even power so, we take 76
= 76 * 16
= 1216
So, Last two non zero digits of 4^972 are 16.
Example3: Find last 2 digits of 6^600.
Solution:
- step 1:- conversion
6^600 = (2)^600 * (3)^600
= (2^10)^60 * ((3)^4)^150 {Apply case 2 in (3)^600}
- step 2:- (2^10)^60 has even power so, we take 76 as the last digit
- step 3:- Solve ((3)^4)^150, we get 01 as the last digit
- step 4:- last digit of (2^10)^60 i.e 76 multiply with the last digit of ((3)^4)^150 i.e 01
- step 5:- i.e 76 * 01 = 76
So, Last two non zero of 6^600 is 76.
Example4: Find last 2 digits of 8^330.
Solution:
- step 1:- conversion
8^33 = (2^3)^110
= (2)^330
- step 2:- (2^10)^33 has odd power so, we take 24 as the last digit
So, Last two non zero digits of 8^330 are 24.
- Case 4: when x ends with 5
For finding the last two digit of a number, when the number ends with 5 then we have to follow the table which is given below.

Example1: Find last 2 digit of 25^25.
Solution:
- first digit of number is 2 i.e even
- Last digit of a power is 5 i.e odd
- Now, even-odd combination gives last digit as a 25
So, the last two non zero digits of 25^25 are 25.
Example2: Find last 2 digit of 25^222.
Solution:
- first digit of number is 2 i.e even
- Last digit of a power is 2 i.e even
- Now, even-even combination gives last digit as a 25
So, the last two non zero digits of 25^222 are 25.
Example3: Find last 2 digit of 165^222.
Solution:
- first digit of number is 1 i.e odd
- Last digit of a power is 2 i.e even
- Now, odd-even combination gives last digit as a 25
So, the last two non zero digits of 165^222 are 25.
Example4: Find last 2 digit of 165^221.
Solution:
- first digit of number is 1 i.e odd
- Last digit of a power is 1 i.e odd
- Now, odd-odd combination gives last digit as a 75
So, the last two non zero digits of 165^221 are 75.
- Case 5: when x ends with 0
For finding the last two digit of a number, when the number ends with 0 then we have to check next digit and according to the digit calculate the last digit.
Example: Find last 2 digit of 150^221.
Solution:
- 150 last digit is 0 so we check next digit i.e 5 and apply case 4
- first digit of number is 1 i.e odd
- Last digit of a power is 1 i.e odd
- Now, odd-odd combination gives last digit as a 75
So, the last two non zero digits of 165^221 is 75.