Program to find the Hidden Number
Last Updated :
02 Sep, 2022
Given an array of 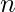 integers, The task is to find another integer
integers, The task is to find another integer 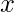 such that, if all the elements of the array are subtracted individually from the number
such that, if all the elements of the array are subtracted individually from the number 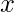 , then the sum of all the differences should add to 0. If any such integer exists, print the value of
, then the sum of all the differences should add to 0. If any such integer exists, print the value of 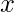 , else print
, else print 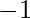 .
.
Example
Input: arr[] = {1, 2, 3}
Output: 2
Explanation:
Subtracting all the elements of arrays from 2,
The sum of difference is:
1 + 0 + (-1) = 0.
Solution: The idea is to calculate the total sum of the array and divide it by the size of the array. If the sum of the array is perfectly divisible by its size then the quotient obtained from this division operation will be the required hidden number.
Implementation:
C++
#include <iostream>
using namespace std;
int main() {
int n = 3;
int a[] = { 1, 2, 3 };
int i = 0;
long sum = 0;
for (i = 0; i < n; i++) {
sum += a[i];
}
long x = sum / n;
if (x * n == sum)
cout<<x<<endl;
else
cout<<("-1")<<endl;
return 0;
}
|
Java
public class GFG {
public static void main(String args[])
{
int n = 3;
int a[] = { 1, 2, 3 };
int i = 0;
long sum = 0;
for (i = 0; i < n; i++) {
sum += a[i];
}
long x = sum / n;
if (x * n == sum)
System.out.println(x);
else
System.out.println("-1");
}
}
|
Python 3
if __name__ == "__main__":
n = 3
a = [ 1, 2, 3 ]
i = 0
sum = 0
for i in range(n):
sum += a[i]
x = sum // n
if (x * n == sum):
print(x)
else:
print("-1")
|
C#
using System;
class GFG
{
public static void Main()
{
int n = 3;
int []a = { 1, 2, 3 };
int i = 0;
long sum = 0;
for (i = 0; i < n; i++)
{
sum += a[i];
}
long x = sum / n;
if (x * n == sum)
Console.WriteLine(x);
else
Console.WriteLine("-1");
}
}
|
PHP
<?php
$n = 3;
$a = array( 1, 2, 3 );
$i = 0;
$sum = 0;
for ($i = 0; $i < $n; $i++)
{
$sum += $a[$i];
}
$x = $sum / $n;
if ($x * $n == $sum)
echo($x);
else
echo("-1");
?>
|
Javascript
<script>
let n = 3;
let a=[1, 2, 3];
let i = 0;
let sum = 0;
for (i = 0; i < n; i++) {
sum += a[i];
}
let x = sum / n;
if (x * n == sum)
document.write(x);
else
document.write("-1");
</script>
|
Complexity Analysis:
- Time Complexity: O(n), where n is the length of the given array.
- Auxiliary space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...