Program to find the Eccentricity of an Ellipse
Last Updated :
04 May, 2021
Given two positive integers A and B, representing the length of the semi-major and semi-minor axis of an ellipse of the equation 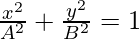 , the task is to find the eccentricity of the given ellipse.
, the task is to find the eccentricity of the given ellipse.
Examples:
Input: A = 12, B = 9
Output: 0.66
Input: A = 6, B = 3
Output: 0.87
Approach: The given problem can be solved based on the following formula to calculate the eccentricity of an ellipse which is given by:
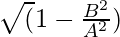
where,
A = Length of semi major axis
B = Length of semi minor axis

Therefore, print the value of 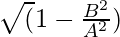 as the eccentricity of the ellipse.
as the eccentricity of the ellipse.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findEccentricity(double A,
double B)
{
double semiMajor = A * A;
double semiMinor = B * B;
double ans = sqrt(1 - semiMinor / semiMajor);
cout << fixed << setprecision(2)
<< ans;
}
int main()
{
double A = 12, B = 9;
findEccentricity(A, B);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void findEccentricity(double A, double B)
{
double semiMajor = A * A;
double semiMinor = B * B;
double ans = Math.sqrt(1 - semiMinor / semiMajor);
System.out.format("%.2f", ans);
}
public static void main(String arr[])
{
double A = 12, B = 9;
findEccentricity(A, B);
}
}
|
Python3
import math
def findEccentricity(A, B):
semiMajor = A * A
semiMinor = B * B
ans = math.sqrt(1 - semiMinor / semiMajor)
print('%.2f' % ans)
if __name__ == "__main__":
A = 12
B = 9
findEccentricity(A, B)
|
C#
using System;
class GFG{
static void findEccentricity(double A, double B)
{
double semiMajor = A * A;
double semiMinor = B * B;
double ans = Math.Sqrt(1 - semiMinor / semiMajor);
Console.Write(Math.Round(ans, 2));
}
static void Main()
{
double A = 12, B = 9;
findEccentricity(A, B);
}
}
|
Javascript
<script>
function findEccentricity(A, B)
{
var semiMajor = A * A;
var semiMinor = B * B;
var ans = Math.sqrt(1 - semiMinor / semiMajor)
return ans.toFixed(2);
}
var A = 12;
var B = 9;
document.write(findEccentricity(A, B));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...