Program to find the Break Even Point
Last Updated :
11 Jul, 2022
Given the list of monthly expenditure
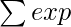
of an organization, selling price
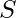
and the overhead maintenance
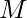
of each item, the task is to calculate the Break Even Point.
Break Even Point refers to the number of items sold in order to neutralize the total expenditure i.e. Overall, neither profit nor loss.
Examples:
Input: Expenditure = 18000, S = 600, M = 100
Output: 36
We need to sell 36 items to cover expenditure and maintenance overhead
Input: Expenditure = 3550, S = 90, M = 65
Output: 142
Approach:
- Calculate the sum of all the expenditures.
- Subtract the maintenance (Cost price) from the selling price.
- Divide the expenditure sum by the above-obtained amount to get the minimum number of items to be sold (Break Even Point).
Below is the implementation of the above approach:
C++
#include <iostream>
#include <math.h>
using namespace std;
int breakEvenPoint(int exp, int S, int M)
{
float earn = S - M;
int res = ceil(exp / earn);
return res;
}
int main()
{
int exp = 3550, S = 90, M = 65;
cout << breakEvenPoint(exp, S, M);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
class GFG
{
public static int breakEvenPoint(int exp1,
int S, int M)
{
double earn = S - M;
double exp = exp1;
double res = Math.ceil(exp / earn);
int res1 = (int) res;
return res1;
}
public static void main (String[] args)
{
int exp = 3550, S = 90, M = 65;
System.out.println(breakEvenPoint(exp, S, M));
}
}
|
Python 3
import math
def breakEvenPoint(exp, S, M):
earn = S - M
if res != 0:
res = math.ceil(exp / earn)
else:
res = float('inf')
return res
if __name__ == "__main__" :
exp = 3550
S = 90
M = 65
print (int(breakEvenPoint(exp, S, M)))
|
C#
using System;
class GFG
{
public static int breakEvenPoint(int exp1,
int S, int M)
{
double earn = S - M;
double exp = exp1;
double res = Math.Ceiling(exp / earn);
int res1 = (int) res;
return res1;
}
public static void Main ()
{
int exp = 3550, S = 90, M = 65;
Console.WriteLine(breakEvenPoint(exp, S, M));
}
}
|
PHP
<?php
function breakEvenPoint($exp, $S, $M)
{
$earn = $S - $M;
$res = ceil($exp / $earn);
return $res;
}
$exp = 3550; $S = 90; $M = 65;
echo breakEvenPoint($exp, $S, $M);
?>
|
Javascript
<script>
function breakEvenPoint(exp, S, M)
{
var earn = S - M;
var res = Math.ceil(exp / earn);
return res;
}
var exp = 3550, S = 90, M = 65;
document.write( breakEvenPoint(exp, S, M));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...