Program to find slant height of cone and pyramid

Given two integers H1 and R representing the height and radius of a cone and two integers H2 and S representing the height and length of base of a pyramid, the task is to find the slant height of the cone and the pyramid.

Examples: 

Input: H1 = 4.5, R = 6, H2 = 4, S = 4.8
Output:
Slant height of cone is: 7.5
Slant height of pyramid is: 4.66476

Input: H1 = 2, R = 4, H2 = 4, S = 8
Output:
Slant height of cone is: 4.47214
Slant height of pyramid is: 5.65685

Approach: The slant height of an object such as a cone or a pyramid is the distance measured from any vertex along a lateral face to the base (along the center of the face). The slant height of a right circular cone is uniform throughout the surface and is given by the formula:

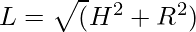
where, 
L is the slant height of the right circular cone
R is the radius of the right circular cone and
H is the height of the right circular cone

The slant height of a pyramid is given by the formula:

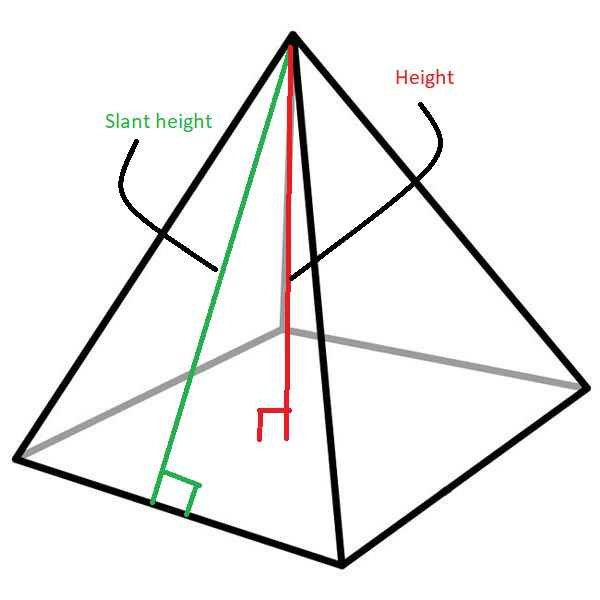
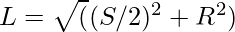
where, 
L is the slant height of the pyramid
S is the side of the base of the pyramid
H is the height of the pyramid

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to calculate slant
// height of a cone
void coneSlantHeight(double cone_h,
                     double cone_r)
{
    // Store the slant height of cone
    double slant_height_cone
        = sqrt(pow(cone_h, 2)
               + pow(cone_r, 2));

    // Print the result
    cout << "Slant height of cone is: "
         << slant_height_cone << '\n';
}

// Function to find the slant
// height of a pyramid
void pyramidSlantHeight(double pyramid_h,
                        double pyramid_s)
{

    // Store the slant height of pyramid
    double slant_height_pyramid
        = sqrt(pow(pyramid_s / 2, 2)
               + pow(pyramid_h, 2));

    // Print the result
    cout << "Slant height of pyramid is: "
         << slant_height_pyramid << '\n';
}

// Driver Code
int main()
{
    // Dimensions of Cone
    double H1 = 4.5, R = 6;

    // Function Call for slant height
    // of Cone
    coneSlantHeight(H1, R);

    // Dimensions of Pyramid
    double H2 = 4, S = 4.8;

    // Function to calculate
    // slant height of a pyramid
    pyramidSlantHeight(H2, S);

    return 0;
}

Java

// Java program for the above approach
import java.io.*;
class GFG
{

    // Function to calculate slant
    // height of a cone
    static void coneSlantHeight(double cone_h,
                         double cone_r)
    {

        // Store the slant height of cone
        double slant_height_cone
            = Math.sqrt(Math.pow(cone_h, 2)
                   + Math.pow(cone_r, 2));

        // Print the result
        System.out.println("Slant height of cone is: " +
        slant_height_cone);
    }

    // Function to find the slant
    // height of a pyramid
    static void pyramidSlantHeight(double pyramid_h,
                            double pyramid_s)
    {

        // Store the slant height of pyramid
        double slant_height_pyramid
            = Math.sqrt(Math.pow(pyramid_s / 2, 2)
                   + Math.pow(pyramid_h, 2));

        // Print the result
        System.out.println("Slant height of pyramid is: " +
        slant_height_pyramid);
    }

    // Driver Code
    public static void main (String[] args)
    {

        // Dimensions of Cone
        double H1 = 4.5, R = 6;

        // Function Call for slant height
        // of Cone
        coneSlantHeight(H1, R);

        // Dimensions of Pyramid
        double H2 = 4, S = 4.8;

        // Function to calculate
        // slant height of a pyramid
        pyramidSlantHeight(H2, S);

    }
}

// This code is contributed by AnkThon

Python3

# Python 3 program for the above approach
from math import sqrt,pow
# Function to calculate slant
# height of a cone
def coneSlantHeight(cone_h, cone_r):
  # Store the slant height of cone
  slant_height_cone = sqrt(pow(cone_h, 2) + pow(cone_r, 2))

  # Print the result
  print("Slant height of cone is:",slant_height_cone)

# Function to find the slant
# height of a pyramid
def pyramidSlantHeight(pyramid_h, pyramid_s):
  # Store the slant height of pyramid
  slant_height_pyramid = sqrt(pow(pyramid_s/2, 2) + pow(pyramid_h, 2))

   # Print the result
  print("Slant height of pyramid is:","{:.5f}".format(slant_height_pyramid))

# Driver Code
if __name__ == '__main__':
  # Dimensions of Cone
  H1 = 4.5
  R = 6

  # Function Call for slant height
  # of Cone
  coneSlantHeight(H1, R);

  # Dimensions of Pyramid
  H2 = 4
  S = 4.8

  # Function to calculate
  # slant height of a pyramid
  pyramidSlantHeight(H2, S)

C#

// C# program for the above approach
using System;
public class GFG
{

  // Function to calculate slant
  // height of a cone
  static void coneSlantHeight(double cone_h,
                              double cone_r)
  {

    // Store the slant height of cone
    double slant_height_cone
      = Math.Sqrt(Math.Pow(cone_h, 2)
                  + Math.Pow(cone_r, 2));

    // Print the result
    Console.WriteLine("Slant height of cone is: " +
                      slant_height_cone);
  }

  // Function to find the slant
  // height of a pyramid
  static void pyramidSlantHeight(double pyramid_h,
                                 double pyramid_s)
  {

    // Store the slant height of pyramid
    double slant_height_pyramid
      = Math.Sqrt(Math.Pow(pyramid_s / 2, 2)
                  + Math.Pow(pyramid_h, 2));

    // Print the result
    Console.WriteLine("Slant height of pyramid is: " +
                      slant_height_pyramid);
  }

  // Driver Code
  public static void Main (string[] args)
  {

    // Dimensions of Cone
    double H1 = 4.5, R = 6;

    // Function Call for slant height
    // of Cone
    coneSlantHeight(H1, R);

    // Dimensions of Pyramid
    double H2 = 4, S = 4.8;

    // Function to calculate
    // slant height of a pyramid
    pyramidSlantHeight(H2, S);

  }
}

// This code is contributed by AnkThon

Javascript

<script>

// javascript program for the above approach


  // Function to calculate slant
  // height of a cone

  function coneSlantHeight( cone_h,
                            cone_r)
  {

    // Store the slant height of cone

    var slant_height_cone =
    Math.sqrt(Math.pow(cone_h, 2) +
    Math.pow(cone_r, 2));

    // Print the result

    document.write("Slant height of cone is: "
            + slant_height_cone + "<br>");
  }

  // Function to find the slant
  // height of a pyramid
   function pyramidSlantHeight( pyramid_h, pyramid_s)
  {

    // Store the slant height of pyramid

 var slant_height_pyramid =
 Math.sqrt(Math.pow(pyramid_s / 2, 2) +
 Math.pow(pyramid_h, 2));

    document.write("Slant height of pyramid is: "
             + slant_height_pyramid.toFixed(5));
  }


  // Driver Code


    // Dimensions of Cone

    var H1 = 4.5, R = 6;

    // Function Call for slant height
    // of Cone
    coneSlantHeight(H1, R);

    // Dimensions of Pyramid
    var H2 = 4, S = 4.8;

    // Function to calculate
    // slant height of a pyramid
    pyramidSlantHeight(H2, S);

</script>

Output:

Slant height of cone is: 7.5
Slant height of pyramid is: 4.66476

Time Complexity: O(sqrt(logH1+logR) + sqrt(logH2+logS))
Auxiliary Space: O(1)