Program to find HCF (Highest Common Factor) of 2 Numbers

HCF (Highest Common Factor) or GCD (Greatest Common Divisor) of two numbers is the largest number that divides both of them. 

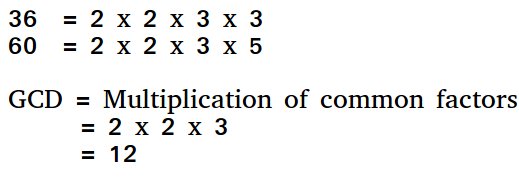
For example, GCD of 20 and 28 is 4, and GCD of 98 and 56 is 14.

A simple solution is to find all prime factors of both numbers, then find the intersection of all factors present in both numbers. Finally, return the product of elements in the intersection.

An efficient solution is to use Euclidean algorithm which is the main algorithm used for this purpose. The idea is, GCD of two numbers doesn’t change if smaller number is subtracted from a bigger number. 

C++

// C++ program to find GCD of two numbers
#include <iostream>
using namespace std;

// Recursive function to return gcd of a and b
int gcd(int a, int b)
{

    // Everything divides 0
    if (a == 0 && b == 0)
        return 0;
    if (a == 0)
        return b;
    if (b == 0)
        return a;

    // base case
    if (a == b)
        return a;

    // a is greater
    if (a > b)
        return gcd(a - b, b);
    return gcd(a, b - a);
}

// Driver program to test above function
int main()
{
    int a = 0, b = 56;
    cout << "GCD of " << a << " and " << b <<  " is " << gcd(a, b);
    return 0;
}

// This code is contributed by shivanisinghss2110

C

// C program to find GCD of two numbers
#include <stdio.h>

// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
    // Everything divides 0
    if (a == 0 && b == 0)
        return 0;
    if (a == 0)
        return b;
    if (b == 0)
        return a;

    // base case
    if (a == b)
        return a;

    // a is greater
    if (a > b)
        return gcd(a - b, b);
    return gcd(a, b - a);
}

// Driver program to test above function
int main()
{
    int a = 0, b = 56;
    printf("GCD of %d and %d is %d ", a, b, gcd(a, b));
    return 0;
}

Java

// Java program to find GCD of two numbers
import java.io.*;

class Test {
    // Recursive function to return gcd of a and b
    static int gcd(int a, int b)
    {
        // Everything divides 0
        if (a == 0 && b == 0)
            return 0;
        if (a == 0)
            return b;
        if (b == 0)
            return a;

        // base case
        if (a == b)
            return a;

        // a is greater
        if (a > b)
            return gcd(a - b, b);
        return gcd(a, b - a);
    }

    // Driver method
    public static void main(String[] args)
    {
        int a = 98, b = 56;
        System.out.println("GCD of " + a + " and " + b
                           + " is " + gcd(a, b));
    }
}

Python3

# Recursive function to return gcd of a and b
def gcd(a, b):

    # Everything divides 0
    if(a == 0 and b == 0):
        return 0

    if(a == 0):
        return b

    if(b == 0):
        return a

    # base case
    if(a == b):
        return a

    # a is greater
    if (a > b):
        return gcd(a-b, b)
    return gcd(a, b-a)

# Driver program to test above function
a = 98
b = 56
if(gcd(a, b)):
    print('GCD of', a, 'and', b, 'is', gcd(a, b))
else:
    print('not found')

# This code is contributed by Danish Raza

C#

// C# program to find GCD of two
// numbers
using System;

class GFG {

    // Recursive function to return
    // gcd of a and b
    static int gcd(int a, int b)
    {

        // Everything divides 0
        if (a == 0 && b == 0)
            return 0;
        if (a == 0)
            return b;
        if (b == 0)
            return a;

        // base case
        if (a == b)
            return a;

        // a is greater
        if (a > b)
            return gcd(a - b, b);

        return gcd(a, b - a);
    }

    // Driver method
    public static void Main()
    {
        int a = 98, b = 56;
        Console.WriteLine("GCD of " + a + " and " + b
                          + " is " + gcd(a, b));
    }
}

// This code is contributed by anuj_67.

PHP

<?php
// PHP program to find GCD
// of two numbers

// Recursive function to
// return gcd of a and b
function gcd($a, $b)
{
    // Everything divides 0
    if($a==0 && $b==0)
        return 0 ;

    if($a == 0)
      return $b;

    if($b == 0)
      return $a;

    // base case
    if($a == $b)
        return $a ;

    // a is greater
    if($a > $b)
        return gcd( $a-$b , $b ) ;

    return gcd( $a , $b-$a ) ;
}

// Driver code
$a = 98 ;
$b = 56 ;

echo "GCD of $a and $b is ", gcd($a , $b) ;

// This code is contributed by Anivesh Tiwari
?>

Javascript

<script>

// Javascript program to find GCD of two numbers

// Recursive function to return gcd of a and b
function gcd(a, b)
{

    // Everything divides 0
    if (a == 0 && b == 0)
        return 0;
    if (a == 0)
        return b;
    if (b == 0)
        return a;

    // Base case
    if (a == b)
        return a;

    // a is greater
    if (a > b)
        return gcd(a - b, b);

    return gcd(a, b - a);
}

// Driver code
var a = 98, b = 56;

document.write("GCD of " + a + " and " +
                  b + " is " +  gcd(a, b));

// This code is contributed by noob2000

</script>

Output

GCD of 0 and 56 is 56

Time Complexity: O(max(a,b)), where a and b are the given two integers.
Auxiliary Space: O(max(a,b)), where a and b are the given two integers.

A more efficient solution is to use modulo operator in Euclidean algorithm . 

C++

// C++ program to find GCD of two numbers
#include <iostream>
using namespace std;

// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}

// Driver program to test above function
int main()
{
    int a = 98, b = 56;
    cout<<"GCD of " <<a << " and "<< b << " is " << gcd(a, b);
    return 0;
}

// This code is contributed by shivanisinghss2110

C

// C program to find GCD of two numbers
#include <stdio.h>

// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}

// Driver program to test above function
int main()
{
    int a = 98, b = 56;
    printf("GCD of %d and %d is %d ", a, b, gcd(a, b));
    return 0;
}

Java

// Java program to find GCD of two numbers
import java.io.*;

class Test {
    // Recursive function to return gcd of a and b
    static int gcd(int a, int b)
    {
        if (b == 0)
            return a;
        return gcd(b, a % b);
    }

    // Driver method
    public static void main(String[] args)
    {
        int a = 98, b = 56;
        System.out.println("GCD of " + a + " and " + b
                           + " is " + gcd(a, b));
    }
}

Python3

# Recursive function to return gcd of a and b
def gcd(a,b):

    # Everything divides 0
    if (b == 0):
         return a
    return gcd(b, a%b)

# Driver program to test above function
a = 98
b = 56
if(gcd(a, b)):
    print('GCD of', a, 'and', b, 'is', gcd(a, b))
else:
    print('not found')

# This code is contributed by Danish Raza

C#

// C# program to find GCD of two
// numbers
using System;

class GFG {

    // Recursive function to return
    // gcd of a and b
    static int gcd(int a, int b)
    {
       if (b == 0)
          return a;
       return gcd(b, a % b);
    }

    // Driver method
    public static void Main()
    {
        int a = 98, b = 56;
        Console.WriteLine("GCD of "
          + a +" and " + b + " is "
                      + gcd(a, b));
    }
}

// This code is contributed by anuj_67.

PHP

<?php
// PHP program to find GCD
// of two numbers

// Recursive function to
// return gcd of a and b
function gcd($a, $b)
{
    // Everything divides 0
    if($b==0)
        return $a ;

    return gcd( $b , $a % $b ) ;
}

// Driver code
$a = 98 ;
$b = 56 ;

echo "GCD of $a and $b is ", gcd($a , $b) ;

// This code is contributed by Anivesh Tiwari
?>

Javascript

<script>

// Javascript program to find GCD of two numbers

// Recursive function to return gcd of a and b
function gcd(a, b)
{
    if (b == 0)
        return a;

    return gcd(b, a % b);
}

// Driver code
var a = 98, b = 56;

document.write("GCD of " + a +" and " + b +
                  " is " + gcd(a, b));

// This code is contributed by Ankita saini

</script>

Output

GCD of 98 and 56 is 14

Time Complexity: O(log(max(a,b)), where a and b are the given two integers.
Auxiliary Space: O(log(max(a,b)), where a and b are the given two integers.

Please refer GCD of more than two (or array) numbers to find HCF of more than two numbers.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above