Program to find all possible triangles having same Area and Perimeter
Last Updated :
09 Dec, 2022
The task is to find all possible triangles having the same perimeter and area.
Examples:
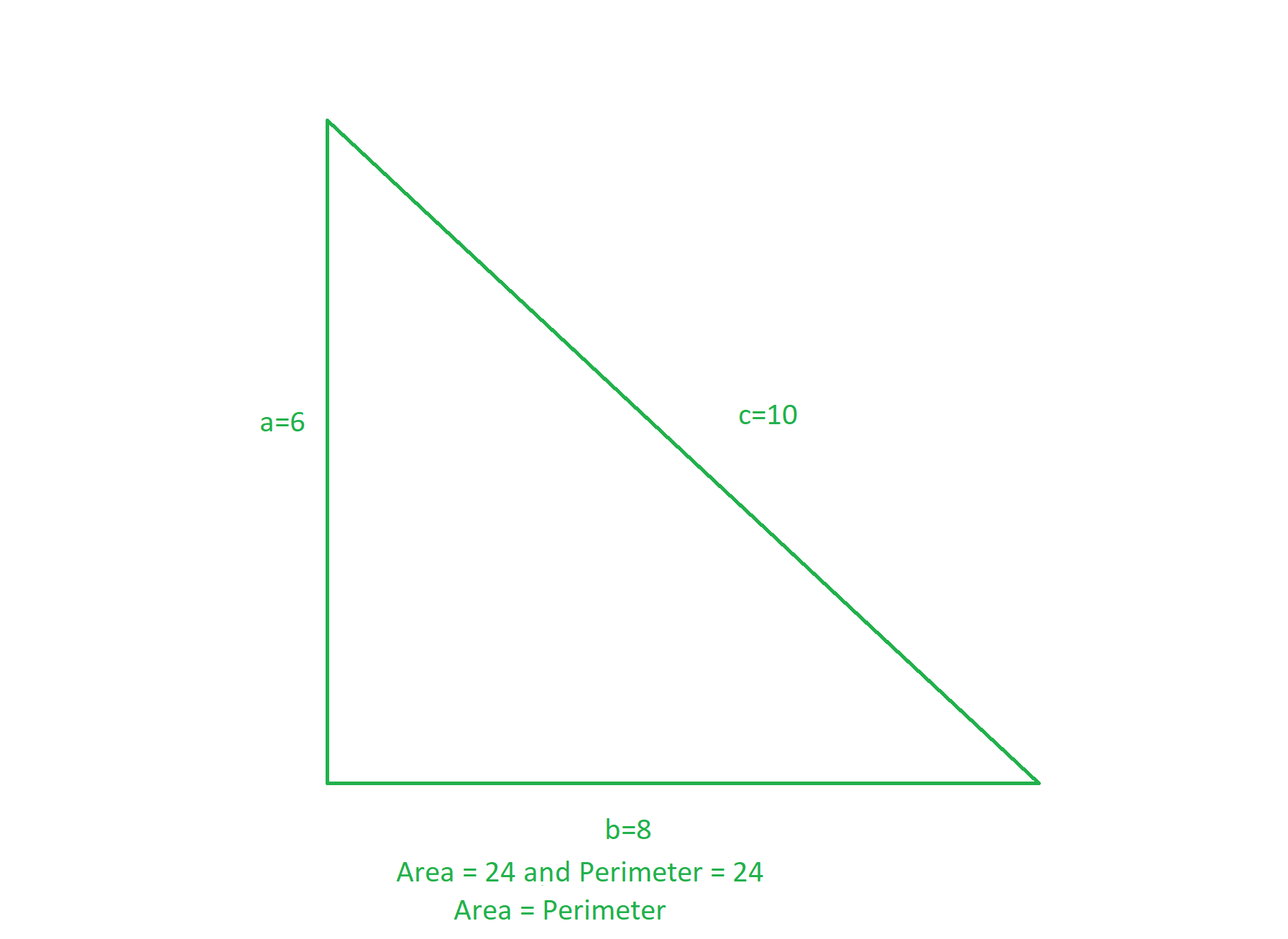
The triangle having sides (6, 8, 10) have the same perimeter (= (6 + 8 + 10) = 24) and area (= 0.5 * 6 * 8 = 24).
Approach: The idea is based on the observation from Heron’s Formula. Below are the observations:
Let the sides of the triangle be a, b, c.
Perimeter(P) = a + b + c
Area(A) using Heron’s Formula:
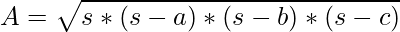
where s = (a + b + c) / 2
Experimental Observation:
We know that:
4 * s2 = s * (s – a) * (s – b) * (s – c)
=> 4 * s = (s – a) * (s – b) * (s – c)
=> 2 * 2 * 2 * 4 * s = 2 * (s – a) * 2 * (s -b) * 2 * (s – c)
=> 16 * (a + b + c) = (- a + b + c) * (a – b + c) * (a + b – c)
Due to this condition:
Max value of (- a + b + c), (a – b + c), (a + b – c) is as follows:
(- a + b + c) * (a – b + c) * (a + b – c) ? 16 * 16 * 16
=> 16 * (a + b + c) ? 16 * 16 * 16
=> (a + b + c) ? 256
From the above equation, the sum of sides of the triangle doesn’t exceed 256 whose perimeter of triangle and area of the triangle can be the same. Therefore, the idea is to iterate three nested loops over the range [1, 256] and print those triplets of sides having the same area and perimeter.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void samePerimeterAndArea()
{
set<vector<int> > se;
for (int i = 1; i <= 256; ++i) {
for (int j = 1; j <= 256; ++j) {
for (int k = 1; k <= 256; ++k) {
int peri = i + j + k;
int mul1 = -i + j + k;
int mul2 = i - j + k;
int mul3 = i + j - k;
if (16 * peri == mul1 * mul2 * mul3) {
vector<int> v = { i, j, k };
sort(v.begin(), v.end());
se.insert(v);
}
}
}
}
for (auto it : se) {
cout << it[0] << " "
<< it[1] << " "
<< it[2] << endl;
}
}
int main()
{
samePerimeterAndArea();
return 0;
}
|
Java
import java.io.*;
import java.util.*;
public class GFG {
static void samePerimeterAndArea()
{
Set<ArrayList<Integer>> se = new HashSet<ArrayList<Integer>>();
for (int i = 1; i <= 256; ++i) {
for (int j = 1; j <= 256; ++j) {
for (int k = 1; k <= 256; ++k) {
int peri = i + j + k;
int mul1 = -i + j + k;
int mul2 = i - j + k;
int mul3 = i + j - k;
if (16 * peri == mul1 * mul2 * mul3) {
ArrayList<Integer> v=new ArrayList<Integer>();
v.add(i);
v.add(j);
v.add(k);
Collections.sort(v);
se.add(v);
}
}
}
}
for (ArrayList<Integer> it : se) {
System.out.println(it.get(0) + " " + it.get(1) + " " + it.get(2));
}
}
public static void main(String[] args)
{
samePerimeterAndArea();
}
}
|
Python3
def samePerimeterAndArea():
se = []
for i in range(1, 256, 1):
for j in range(1, 256, 1):
for k in range(1, 256, 1):
peri = i + j + k
mul1 = -i + j + k
if (k > 100):
break
if (j > 100):
break
if (i > 100):
break
mul2 = i - j + k
mul3 = i + j - k
if (16 * peri == mul1 * mul2 * mul3):
v = [i, j, k]
v.sort(reverse = False)
se.append(v)
se.sort(reverse = False)
temp = []
temp.append(se[0])
temp.append(se[6])
temp.append(se[12])
temp.append(se[18])
temp.append(se[24])
for it in temp:
print(it[0], it[1], it[2])
if __name__ == '__main__':
samePerimeterAndArea()
|
C#
using System;
using System.Collections.Generic;
public class GFG {
static void samePerimeterAndArea()
{
HashSet<Tuple<int, int, int>> se = new HashSet<Tuple<int, int, int>>();
for (int i = 1; i <= 256; ++i) {
for (int j = 1; j <= 256; ++j) {
for (int k = 1; k <= 256; ++k) {
int peri = i + j + k;
int mul1 = -i + j + k;
int mul2 = i - j + k;
int mul3 = i + j - k;
if (16 * peri == mul1 * mul2 * mul3) {
List<int> v=new List<int>();
v.Add(i);
v.Add(j);
v.Add(k);
v.Sort();
Tuple<int, int, int> t = Tuple.Create(v[0], v[1], v[2]);
se.Add(t);
}
}
}
}
foreach (var it in se) {
Console.WriteLine(String.Join(" ", it));
}
}
public static void Main(string[] args)
{
samePerimeterAndArea();
}
}
|
Javascript
<script>
const samePerimeterAndArea = () => {
let se = [];
for(let i = 1; i <= 256; ++i)
{
for(let j = 1; j <= 256; ++j)
{
for(let k = 1; k <= 256; ++k)
{
let peri = i + j + k;
let mul1 = -i + j + k;
let mul2 = i - j + k;
let mul3 = i + j - k;
if (16 * peri == mul1 * mul2 * mul3)
{
let v = [i, j, k];
v.sort((a, b) => a - b);
let check = -1;
for(let i = 0; i < se.length; ++i)
{
if (se[i][0] == v[0] &&
se[i][1] == v[1] &&
se[i][2] == v[2])
check = 1;
}
if (check === -1) se.push(v);
}
}
}
}
for(let it = 0; it < se.length; ++it)
{
document.write(`${se[it]}<br/>`);
}
}
samePerimeterAndArea();
</script>
|
Output: 5 12 13
6 8 10
6 25 29
7 15 20
9 10 17
Time Complexity: O(2563)
Auxiliary Space: O(2563)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...