Program to construct a DFA which accepts the language L = {aN | N ≥ 1}

Prerequisite: Finite Automata

Given a string S of size N, the task is to design a Deterministic Finite Automata (DFA) for accepting the language L = {a^N | N ≥ 1}. The regular language L is {a, aa, aaa, aaaaaaa…, }. If the given string follows the given language L, then print “Accepted”. Otherwise, print “Not Accepted”.

Examples:

Input: S = “aaabbb”
Output: Not Accepted
Explanation: String must only contain a.

Input: S = “aa”
Output: Accepted

Approach: The idea by which the automata lead to acceptance of string is stated below in steps:

• The automata will accept all the strings containing only the character ‘a’. If the user tried to input any character other than ‘a’, the machine will reject it.
• Let the state q0 is the initial state represent the set of all strings of length 0, state q1 is the final state represent the set of all strings from 1 to N.
• State q1 contains a self-loop of a which indicates that it can be repeated as required.
• The logic for code is very basic as it has only a for loop which counts the number of a’s in a given string, if the count of a is the same as N then it will be accepted. Otherwise, the string will be rejected.

DFA State Transition Diagram:

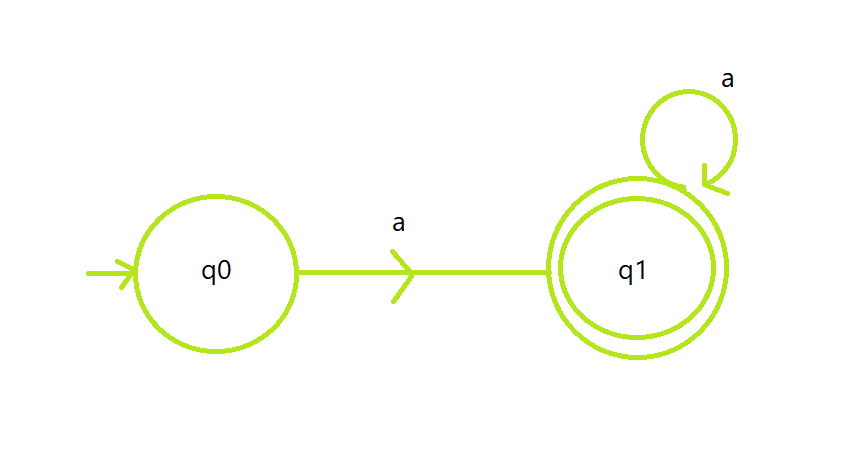
Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to check whether the string
// S satisfy the given DFA or not
void isAcceptedDFA(string s, int N)
{
    // Stores the count of characters
    int count = 0;

    // Iterate over the range [0, N]
    for (int i = 0; i < N; i++) {

        // Count and check every
        // element for 'a'
        if (s[i] == 'a')
            count++;
    }

    // If string matches with DFA
    if (count == N && count != 0) {
        cout << "Accepted";
    }

    // If not matches
    else {
        cout << "Not Accepted";
    }
}

// Driver Code
int main()
{
    string S = "aaaaa";

    // Function Call
    isAcceptedDFA(S, S.size());

    return 0;
}

Java

// Java program for the above approach
class GFG
{

// Function to check whether the String
// S satisfy the given DFA or not
static void isAcceptedDFA(String s, int N)
{
    // Stores the count of characters
    int count = 0;

    // Iterate over the range [0, N]
    for (int i = 0; i < N; i++)
    {

        // Count and check every
        // element for 'a'
        if (s.charAt(i) == 'a')
            count++;
    }

    // If String matches with DFA
    if (count == N && count != 0)
    {
        System.out.print("Accepted");
    }

    // If not matches
    else
    {
        System.out.print("Not Accepted");
    }
}

// Driver Code
public static void main(String[] args)
{
    String S = "aaaaa";

    // Function Call
    isAcceptedDFA(S, S.length());
}
}

// This code is contributed by 29AjayKumar

Python3

# Python3 program for the above approach

# Function to check whether the string
# S satisfy the given DFA or not
def isAcceptedDFA(s, N):

    # Stores the count of characters
    count = 0

    # Iterate over the range [0, N]
    for i in range(N):

        # Count and check every
        # element for 'a'
        if (s[i] == 'a'):
            count += 1

    # If string matches with DFA
    if (count == N and count != 0):
        print ("Accepted")

    # If not matches
    else :
        print ("Not Accepted")

# Driver Code
if __name__ == '__main__':
    S = "aaaaa"

    # Function Call
    isAcceptedDFA(S, len(S))

# This code is contributed by mohit kumar 29

C#

// C# program for the above approach
using System;
class GFG
{

// Function to check whether the String
// S satisfy the given DFA or not
static void isAcceptedDFA(String s, int N)
{

    // Stores the count of characters
    int count = 0;

    // Iterate over the range [0, N]
    for (int i = 0; i < N; i++)
    {

        // Count and check every
        // element for 'a'
        if (s[i] == 'a')
            count++;
    }

    // If String matches with DFA
    if (count == N && count != 0)
    {
        Console.Write("Accepted");
    }

    // If not matches
    else
    {
        Console.Write("Not Accepted");
    }
}

// Driver Code
public static void Main(String[] args)
{
    String S = "aaaaa";

    // Function Call
    isAcceptedDFA(S, S.Length);
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

      // JavaScript program for the above approach
      // Function to check whether the String
      // S satisfy the given DFA or not
      function isAcceptedDFA(s, N) {
        // Stores the count of characters
        var count = 0;

        // Iterate over the range [0, N]
        for (var i = 0; i < N; i++) {
          // Count and check every
          // element for 'a'
          if (s[i] === "a") count++;
        }

        // If String matches with DFA
        if (count === N && count !== 0) {
          document.write("Accepted");
        }

        // If not matches
        else {
          document.write("Not Accepted");
        }
      }

      // Driver Code
      var S = "aaaaa";

      // Function Call
      isAcceptedDFA(S, S.length);

</script>

Output:

Accepted

Time Complexity: O(N)
Auxiliary Space: O(1)