Program to compute log a to any base b (logb a)
Last Updated :
28 Jul, 2023
Given two integers a and b, the task is to find the log of a to any base b, i.e. logb a.
Examples:
Input: a = 3, b = 2
Output: 1
Input: a = 256, b = 4
Output: 4
- Find the log of a to the base 2 with the help of log2() method
- Find the log of b to the base 2 with the help of log2() method
- Divide the computed log a from the log b to get the logb a, i.e,
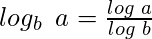
Below is the implementation of the above approach
C++
#include <bits/stdc++.h>
using namespace std;
int log_a_to_base_b(int a, int b)
{
return log2(a) / log2(b);
}
int main()
{
int a = 3;
int b = 2;
cout << log_a_to_base_b(a, b) << endl;
a = 256;
b = 4;
cout << log_a_to_base_b(a, b) << endl;
return 0;
}
|
C
#include <math.h>
#include <stdio.h>
int log_a_to_base_b(int a, int b)
{
return log2(a) / log2(b);
}
int main()
{
int a = 3;
int b = 2;
printf("%d\n",
log_a_to_base_b(a, b));
a = 256;
b = 4;
printf("%d\n",
log_a_to_base_b(a, b));
return 0;
}
|
Java
class GFG
{
static int log_a_to_base_b(int a, int b)
{
return (int)(Math.log(a) / Math.log(b));
}
public static void main (String[] args)
{
int a = 3;
int b = 2;
System.out.println(log_a_to_base_b(a, b));
a = 256;
b = 4;
System.out.println(log_a_to_base_b(a, b));
}
}
|
Python3
from math import log2
def log_a_to_base_b(a, b) :
return log2(a) // log2(b);
if __name__ == "__main__" :
a = 3;
b = 2;
print(log_a_to_base_b(a, b));
a = 256;
b = 4;
print(log_a_to_base_b(a, b));
|
C#
using System;
public class GFG
{
static int log_a_to_base_b(int a, int b)
{
return (int)(Math.Log(a) / Math.Log(b));
}
public static void Main()
{
int a = 3;
int b = 2;
Console.WriteLine(log_a_to_base_b(a, b));
a = 256;
b = 4;
Console.WriteLine(log_a_to_base_b(a, b));
}
}
|
Javascript
<script>
function log_a_to_base_b(a, b)
{
return parseInt(Math.log(a) / Math.log(b));
}
var a = 3;
var b = 2;
document.write(log_a_to_base_b(a, b) + "<br>");
a = 256;
b = 4;
document.write(log_a_to_base_b(a, b));
</script>
|
Time Complexity: O(logba)
Auxiliary Space: O(1)
- Recursively divide a by b till a is greater than b.
- Count the number of times the divide is possible. This is the log of a to the base b, i.e. logb a
Below is the implementation of the above approach
C++
#include <iostream>
using namespace std;
int log_a_to_base_b(int a, int b)
{
return (a > b - 1)
? 1 + log_a_to_base_b(a / b, b)
: 0;
}
int main()
{
int a = 3;
int b = 2;
cout << log_a_to_base_b(a, b) << endl;
a = 256;
b = 4;
cout << log_a_to_base_b(a, b) << endl;
return 0;
}
|
C
#include <stdio.h>
int log_a_to_base_b(int a, int b)
{
return (a > b - 1)
? 1 + log_a_to_base_b(a / b, b)
: 0;
}
int main()
{
int a = 3;
int b = 2;
printf("%d\n",
log_a_to_base_b(a, b));
a = 256;
b = 4;
printf("%d\n",
log_a_to_base_b(a, b));
return 0;
}
|
Java
class GFG
{
static int log_a_to_base_b(int a, int b)
{
int rslt = (a > b - 1)? 1 + log_a_to_base_b(a / b, b): 0;
return rslt;
}
public static void main (String[] args)
{
int a = 3;
int b = 2;
System.out.println(log_a_to_base_b(a, b));
a = 256;
b = 4;
System.out.println(log_a_to_base_b(a, b));
}
}
|
Python3
def log_a_to_base_b(a, b) :
rslt = (1 + log_a_to_base_b(a // b, b)) if (a > (b - 1)) else 0;
return rslt;
if __name__ == "__main__" :
a = 3;
b = 2;
print(log_a_to_base_b(a, b));
a = 256;
b = 4;
print(log_a_to_base_b(a, b));
|
C#
using System;
class GFG
{
static int log_a_to_base_b(int a, int b)
{
int rslt = (a > b - 1)? 1 + log_a_to_base_b(a / b, b): 0;
return rslt;
}
public static void Main()
{
int a = 3;
int b = 2;
Console.WriteLine(log_a_to_base_b(a, b));
a = 256;
b = 4;
Console.WriteLine(log_a_to_base_b(a, b));
}
}
|
Javascript
<script>
function log_a_to_base_b(a , b)
{
var rslt = (a > b - 1) ? 1 + log_a_to_base_b(parseInt(a / b), b) : 0;
return rslt;
}
var a = 3;
var b = 2;
document.write(log_a_to_base_b(a, b)+"<br/>");
a = 256;
b = 4;
document.write(log_a_to_base_b(a, b));
</script>
|
Time Complexity: O(logba)
Auxiliary Space: O(logba) Space required for recursive call stack
Approach:
The approach is to repeatedly divide the given number ‘a’ by the base ‘b’ until ‘a’ becomes less than or equal to 1. In each division, we increment the answer by 1. Finally, we return the answer which represents the logarithm of ‘a’ to the base ‘b’.
- Initialize a variable ‘ans’ to 0.
- Repeat the following steps until ‘a’ becomes less than or equal to 1:
a. Divide ‘a’ by ‘b’.
b. Increment ‘ans’ by 1.
- Return ‘ans’ as the result.
C++
#include <bits/stdc++.h>
using namespace std;
int log_a_to_base_b(int a, int b)
{
int ans = 0;
while (a > 1) {
a /= b;
ans++;
}
return ans;
}
int main()
{
int a = 3;
int b = 2;
cout << log_a_to_base_b(a, b) << endl;
a = 256;
b = 4;
cout << log_a_to_base_b(a, b) << endl;
return 0;
}
|
Java
import java.io.*;
public class GFG {
public static int logAToBaseB(int a, int b) {
int ans = 0;
while (a > 1) {
a /= b;
ans++;
}
return ans;
}
public static void main(String[] args) {
int a = 3;
int b = 2;
System.out.println(logAToBaseB(a, b));
a = 256;
b = 4;
System.out.println(logAToBaseB(a, b));
}
}
|
Python3
def log_a_to_base_b(a, b):
ans = 0
while a > 1:
a //= b
ans += 1
return ans
if __name__ == "__main__":
a = 3
b = 2
print(log_a_to_base_b(a, b))
a = 256
b = 4
print(log_a_to_base_b(a, b))
|
C#
using System;
class Program
{
static int LogAToBaseB(int a, int b)
{
int ans = 0;
while (a > 1)
{
a /= b;
ans += 1;
}
return ans;
}
static void Main(string[] args)
{
int a = 3;
int b = 2;
Console.WriteLine(LogAToBaseB(a, b));
a = 256;
b = 4;
Console.WriteLine(LogAToBaseB(a, b));
}
}
|
Javascript
function log_a_to_base_b(a, b) {
let ans = 0;
while (a > 1) {
a = Math.floor(a / b);
ans++;
}
return ans;
}
let a = 3;
let b = 2;
console.log(log_a_to_base_b(a, b));
a = 256;
b = 4;
console.log(log_a_to_base_b(a, b));
|
Time Complexity: O(log a), as in each iteration, ‘a’ is divided by ‘b’.
Space Complexity: O(1), as only a constant amount of extra space is required for storing the ‘ans’ variable.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...