Program to check if N is a Octagonal Number
Last Updated :
22 Dec, 2022
Given a number N, the task is to check if N is an Octagonal Number or not. If the number N is an Octagonal Number then print “Yes” else print “No”.
Octagonal Number is the figure number that represent octagonal. Octagonal Numbers can be formed by placing triangular numbers on the four sides of a square. The first few Octagonal Numbers are 1, 8, 21, 40, 65, 96 …
Examples:
Input: N = 8
Output: Yes
Explanation:
Second octagonal number is 8.
Input: N = 30
Output: No
Approach:
1. The Kth term of the octagonal number is given as
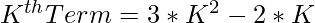
2. As we have to check whether the given number can be expressed as an Octagonal Number or not. This can be checked as:
=> 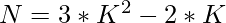
=> 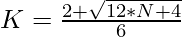
3. If the value of K calculated using the above formula is an integer, then N is an Octagonal Number.
4. Else N is not an Octagonal Number.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isoctagonal(int N)
{
float n
= (2 + sqrt(12 * N + 4))
/ 6;
return (n - (int)n) == 0;
}
int main()
{
int N = 8;
if (isoctagonal(N)) {
cout << "Yes";
}
else {
cout << "No";
}
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
public static boolean isoctagonal(int N)
{
double n = (2 + Math.sqrt(12 * N + 4)) / 6;
return (n - (int)n) == 0;
}
public static void main(String[] args)
{
int N = 8;
if (isoctagonal(N))
{
System.out.println("Yes");
}
else
{
System.out.println("No");
}
}
}
|
Python3
from math import sqrt
def isoctagonal(N):
n = (2 + sqrt(12 * N + 4)) / 6;
return (n - int(n)) == 0;
if __name__ == "__main__":
N = 8;
if (isoctagonal(N)):
print("Yes");
else:
print("No");
|
C#
using System;
class GFG {
public static bool isoctagonal(int N)
{
double n = (2 + Math.Sqrt(12 * N +
4)) / 6;
return (n - (int)n) == 0;
}
public static void Main(String[] args)
{
int N = 8;
if (isoctagonal(N))
{
Console.WriteLine("Yes");
}
else
{
Console.WriteLine("No");
}
}
}
|
Javascript
<script>
function isoctagonal(N)
{
var n = (2 + Math.sqrt(12 * N + 4)) / 6;
return (n - parseInt(n) == 0);
}
var N = 8;
if (isoctagonal(N)) {
document.write("Yes");
}
else {
document.write("No");
}
</script>
|
Time Complexity: O(log N) as sqrt function is being used
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...