Program to check if N is a Centered Tridecagonal Number
Last Updated :
19 Sep, 2022
Given a number N, the task is to check if N is a Centered Tridecagonal Number or not. If the number N is a Centered Tridecagonal Number then print “Yes” else print “No”.
Centered tridecagonal number represents a dot at the center and other dots surrounding the center dot in the successive tridecagonal(13 sided polygon) layer. The first few Centered tridecagonal numbers are 1, 14, 40, 79 …
Examples:
Input: N = 14
Output: Yes
Explanation:
Second Centered tridecagonal number is 14.
Input: N = 30
Output: No
Approach:
1. The Kth term of the Centered Tridecagonal Number is given as
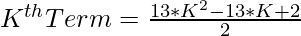
2. As we have to check that the given number can be expressed as a Centered Tridecagonal Number or not. This can be checked as follows:
=> 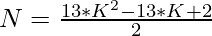
=> 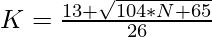
3. If the value of K calculated using the above formula is an integer, then N is a Centered Tridecagonal Number.
4. Else the number N is not a Centered Tridecagonal Number.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isCenteredtridecagonal(int N)
{
float n
= (13 + sqrt(104 * N + 65))
/ 26;
return (n - (int)n) == 0;
}
int main()
{
int N = 14;
if (isCenteredtridecagonal(N)) {
cout << "Yes";
}
else {
cout << "No";
}
return 0;
}
|
Java
class GFG{
static boolean isCenteredtridecagonal(int N)
{
float n = (float) ((13 + Math.sqrt(104 * N +
65)) / 26);
return (n - (int)n) == 0;
}
public static void main(String[] args)
{
int N = 14;
if (isCenteredtridecagonal(N))
{
System.out.print("Yes");
}
else
{
System.out.print("No");
}
}
}
|
Python3
import numpy as np
def isCenteredtridecagonal(N):
n = (13 + np.sqrt(104 * N + 65)) / 26
return (n - int(n)) == 0
N = 14
if (isCenteredtridecagonal(N)):
print ("Yes")
else:
print ("No")
|
C#
using System;
class GFG{
static bool isCenteredtridecagonal(int N)
{
float n = (float) ((13 + Math.Sqrt(104 * N +
65)) / 26);
return (n - (int)n) == 0;
}
public static void Main(string[] args)
{
int N = 14;
if (isCenteredtridecagonal(N))
{
Console.Write("Yes");
}
else
{
Console.Write("No");
}
}
}
|
Javascript
<script>
function isCenteredtridecagonal(N)
{
let n
= (13 + Math.sqrt(104 * N + 65))
/ 26;
return (n - parseInt(n)) == 0;
}
let N = 14;
if (isCenteredtridecagonal(N)) {
document.write("Yes");
}
else {
document.write("No");
}
</script>
|
Time Complexity: O(logN) since inbuilt sqrt function is being used
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...