Program to calculate the area of Kite

Kite is something like rhombus but in Kite, the adjacent sides are equal and diagonals are generally not equal. 

Method 1: When both the diagonals are given

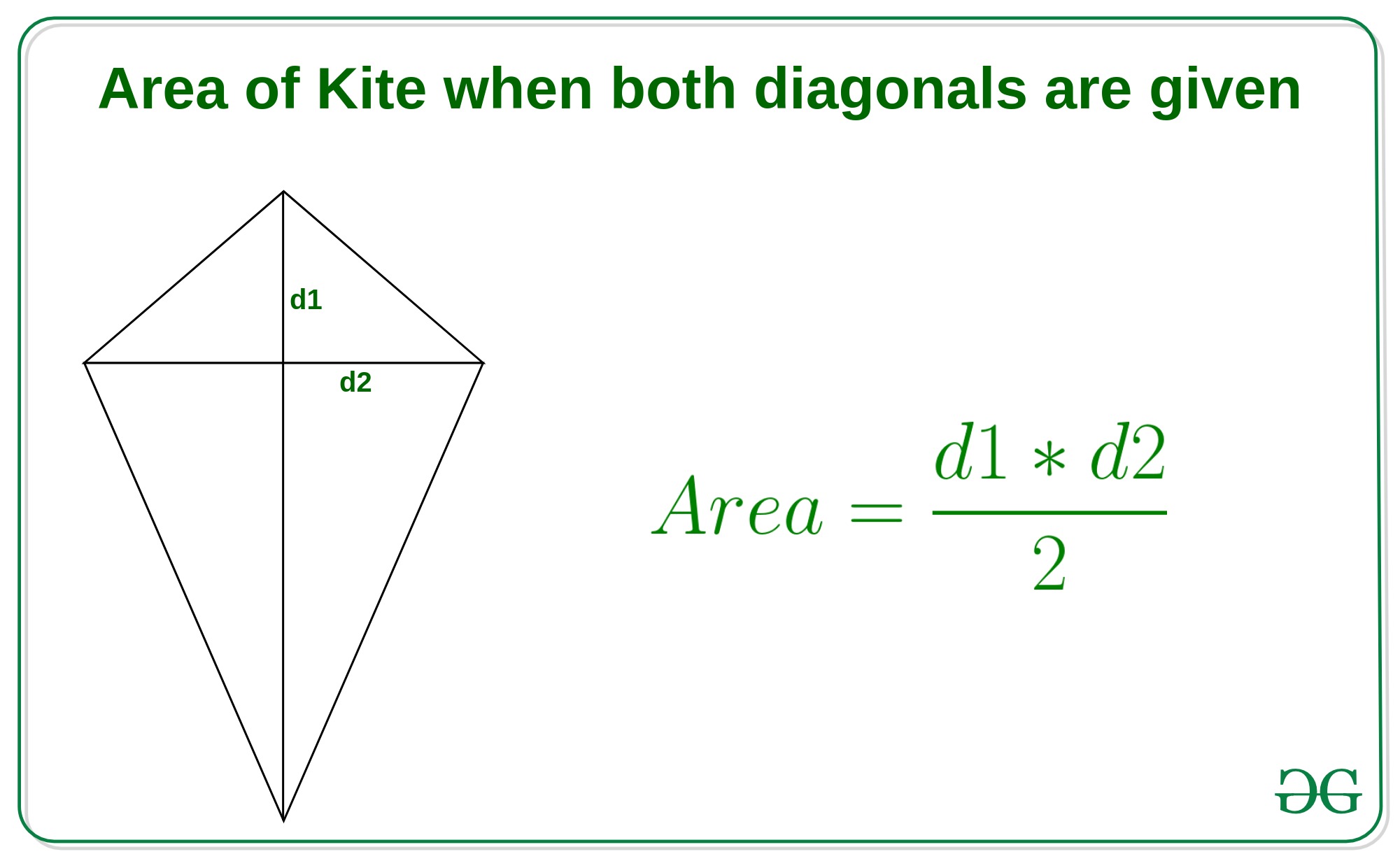
If diagonals d1 and d2 are given of the kite, then the area of a kite is half of product of both the diagonals i.e.

Example:

Input: d1 = 4, d2 = 6
Output: Area of Kite  = 12

Input: d1 = 5, d2 = 7
Output: Area of Kite  = 17.5

Approach: In this method we simply use above formula.
Below is the implementation of the above approach:

C++

// C++ implementation of the approach

#include <bits/stdc++.h>
using namespace std;

// Function to return the area of kite
float areaOfKite(int d1, int d2)
{
    // use above formula
    float area = (d1 * d2) / 2;
    return area;
}

// Driver code
int main()
{
    int d1 = 4, d2 = 6;
    cout << "Area of Kite = "
         << areaOfKite(d1, d2);

    return 0;
}

Java

// Java implementation of the approach
class GFG
{

    // Function to return the area of kite
    static float areaOfKite(int d1, int d2)
    {
        // Use above formula
        float area = (d1 * d2) / 2;
        return area;
    }

    // Driver code
    public static void main(String[] args)
    {
        int d1 = 4, d2 = 6;
        System.out.println("Area of Kite = "
                + areaOfKite(d1, d2));
    }
}

// This code is contributed by Rajput-Ji

Python3

    # Python implementation of the approach

# Function to return the area of kite
def areaOfKite(d1, d2):

    # use above formula
    area = (d1 * d2) / 2;
    return area;

# Driver code
d1 = 4;
d2 = 6;
print("Area of Kite = ",
    areaOfKite(d1, d2));

# This code is contributed by Rajput-Ji

C#

// C# implementation of the approach
using System;

class GFG
{

// Function to return the area of kite
static float areaOfKite(int d1, int d2)
{
    // Use above formula
    float area = (d1 * d2) / 2;
    return area;
}

// Driver code
public static void Main()
{
    int d1 = 4, d2 = 6;
    Console.WriteLine("Area of Kite = "
            + areaOfKite(d1, d2));
}
}

// This code is contributed by anuj_67..

Javascript

<script>

// Javascript implementation of the approach

// Function to return the area of kite
function areaOfKite(d1, d2)
{
    // use above formula
    var area = (d1 * d2) / 2;
    return area;
}

// Driver code
var d1 = 4, d2 = 6;
document.write("Area of Kite = "
    + areaOfKite(d1, d2));

</script>

Output:

Area of Kite = 12

Time Complexity: O(1)

Auxiliary Space: O(1)

Method 2: When side a, b and angle are given: 

When the unequal sides of kite a and b and the included angle Θ between them are given, then 

Example:

Input: a = 4, b = 7, θ = 78
Output: Area of Kite  = 27.3881

Input: a = 6, b = 9, θ = 83
Output: Area of Kite  = 53.5975

Approach: In this method we simply use above formula.
Below is the implementation of the above approach:

C++

// C++ implementation of the approach

#include <bits/stdc++.h>
#define PI 3.14159 / 180
using namespace std;

// Function to return the area of the kite
float areaOfKite(int a, int b, double angle)
{
    // convert angle degree to radians
    angle = angle * PI;
    // use above formula

    double area = a * b * sin(angle);
    return area;
}

// Driver code
int main()
{
    int a = 4, b = 7, angle = 78;
    cout << "Area of Kite = "
         << areaOfKite(a, b, angle);

    return 0;
}

Java

// Java implementation of the approach
import java.io.*;

class GFG
{

static double PI = (3.14159 / 180);

// Function to return the area of the kite
static float areaOfKite(int a, int b, double angle)
{
    // convert angle degree to radians
    angle = angle * PI;

    // use above formula
    double area = a * b * Math.sin(angle);
    return (float)area;
}

// Driver code
public static void main (String[] args)
{

    int a = 4, b = 7, angle = 78;
    System.out.println ("Area of Kite = " + areaOfKite(a, b, angle));
}
}

// This code is contributed by jit_t.

Python3

# Python implementation of the approach
import math
PI = 3.14159 / 180;

# Function to return the area of the kite
def areaOfKite(a, b, angle):

    # convert angle degree to radians
    angle = angle * PI;

    # use above formula

    area = a * b * math.sin(angle);
    return area;

# Driver code
a = 4; b = 7; angle = 78;
print("Area of Kite = ",
        areaOfKite(a, b, angle));

# This code contributed by PrinciRaj1992

C#

// C# implementation of the approach
using System;

class GFG
{
    static double PI = (3.14159 / 180);

// Function to return the area of the kite
static float areaOfKite(int a, int b, double angle)
{
    // convert angle degree to radians
    angle = angle * PI;

    // use above formula
    double area = a * b * Math.Sin(angle);
    return (float)area;
}

// Driver code
static public void Main ()
{
    int a = 4, b = 7, angle = 78;
    Console.WriteLine("Area of Kite = " + areaOfKite(a, b, angle));
}
}

// This code is contributed by ajit

Javascript

<script>
// Javascript implementation of the approach
var PI = 3.14159 / 180

// Function to return the area of the kite
function areaOfKite(a, b, angle)
{

    // convert angle degree to radians
    angle = angle * PI;
    // use above formula

    var area = a * b * Math.sin(angle);
    return area.toFixed(4);
}

// Driver code
var a = 4, b = 7, angle = 78;
document.write( "Area of Kite = "
     + areaOfKite(a, b, angle));

// This code is contributed by rutvik_56.
</script>

Output:

Area of Kite = 27.3881

Time Complexity: O(1)

Auxiliary Space: O(1)