Program to calculate the Area and Perimeter of Incircle of an Equilateral Triangle

Last Updated : 27 Nov, 2018

Given the length of sides of an equilateral triangle, the task is to find the area and perimeter of Incircle of the given equilateral triangle.

Examples:

Input: side = 6 
Output: Area = 9.4. Perimeter = 10.88

Input: side = 9
Output: Area = 21.21, Perimeter = 16.32

Properties of an Incircle are:

The center of the Incircle is same as the center of the triangle i.e. the point where the medians of the equilateral triangle intersect.
Inscribed circle of an equilateral triangle is made through the midpoint of the edges of an equilateral triangle.
The Inradius of an Incircle of an equilateral triangle can be calculated using the formula:
```
 ,
```
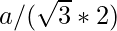where 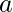$a$ is the length of the side of equilateral triangle.
Below image shows an equilateral triangle with incircle:

Approach:

Area of circle = 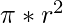$\pi*r^2$ and perimeter of circle = 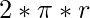$2 * \pi * r$ , where r is the radius of given circle.

Also the radius of Incircle of an equilateral triangle = (side of the equilateral triangle)/ 3.
Therefore,

The formula used to calculate the area of Incircle using Inradius is:
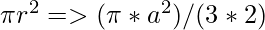
The formula used to calculate the perimeter of Incircle using Inradius is:

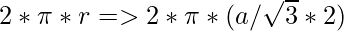
C

// C program to find the area of Inscribed circle  
// of equilateral triangle 
#include <math.h> 
#include <stdio.h> 
#define PI 3.14159265 
  
// function to find area of inscribed circle 
float area_inscribed(float a) 
{ 
    return (a * a * (PI / 12)); 
} 
  
// function to find Perimeter of inscribed circle 
float perm_inscribed(float a) 
{ 
    return (PI * (a / sqrt(3))); 
} 
  
// Driver code 
int main() 
{ 
    float a = 6; 
    printf("Area of inscribed circle is :%f\n", 
           area_inscribed(a)); 
  
    printf("Perimeter of inscribed circle is :%f", 
           perm_inscribed(a)); 
  
    return 0; 
} 

Java

// Java code to find the area of inscribed 
// circle of equilateral triangle 
import java.lang.*; 
  
class GFG { 
  
    static double PI = 3.14159265; 
  
    // function to find the area of 
    // inscribed circle 
    public static double area_inscribed(double a) 
    { 
        return (a * a * (PI / 12)); 
    } 
  
    // function to find the perimeter of 
    // inscribed circle 
    public static double perm_inscribed(double a) 
    { 
        return (PI * (a / Math.sqrt(3))); 
    } 
  
    // Driver code 
    public static void main(String[] args) 
    { 
        double a = 6.0; 
        System.out.println("Area of inscribed circle is :"
                           + area_inscribed(a)); 
  
        System.out.println("\nPerimeter of inscribed circle is :"
                           + perm_inscribed(a)); 
    } 
} 

Python3

# Python3 code to find the area of inscribed  
# circle of equilateral triangle 
import math 
PI = 3.14159265
      
# Function to find the area of  
# inscribed circle 
def area_inscribed(a): 
    return (a * a * (PI / 12)) 
  
# Function to find the perimeter of  
# inscribed circle 
def perm_inscribed(a): 
    return ( PI * (a / math.sqrt(3) ) )     
  
  
# Driver code 
a = 6.0
print("Area of inscribed circle is :% f"
                        % area_inscribed(a)) 
print("\nPerimeter of inscribed circle is :% f"
                        % perm_inscribed(a)) 

C#

// C# code to find the area of 
// inscribed circle 
// of equilateral triangle 
using System; 
  
class GFG { 
    static double PI = 3.14159265; 
  
    // function to find the area of 
    // inscribed circle 
    public static double area_inscribed(double a) 
    { 
        return (a * a * (PI / 12)); 
    } 
  
    // function to find the perimeter of 
    // inscribed circle 
    public static double perm_inscribed(double a) 
    { 
        return (PI * (a / Math.Sqrt(3))); 
    } 
  
    // Driver code 
    public static void Main() 
    { 
        double a = 6.0; 
        Console.Write("Area of inscribed circle is :"
                      + area_inscribed(a)); 
  
        Console.Write("\nPerimeter of inscribed circle is :"
                      + perm_inscribed(a)); 
    } 
} 

PHP

<?php 
// PHP program to find the  
// area of inscribed  
// circle of equilateral triangle 
$PI = 3.14159265; 
  
// function to find area of  
// inscribed circle 
function area_inscribed($a) 
{ 
    global $PI; 
    return ($a * $a * ($PI / 12)); 
} 
  
// function to find perimeter of  
// inscribed circle 
function perm_inscribed($a) 
{ 
    global $PI; 
    return ( $PI * ( $a / sqrt(3) ) ); 
} 
  
// Driver code 
$a = 6; 
echo("Area of inscribed circle is :"); 
echo(area_inscribed($a)); 
echo("Perimeter of inscribed circle is :"); 
echo(perm_inscribed($a)); 
  
?> 

Output:

Area of inscribed circle is :9.424778
Perimeter of inscribed circle is :10.882796

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

My Personal Notes

Related Articles

C

Java

Python3

C#

PHP