Program to calculate sum of an Infinite Arithmetic-Geometric Sequence
Last Updated :
20 Jul, 2022
Given three integers A, D, and R representing the first term, common difference, and common ratio of an infinite Arithmetic-Geometric Progression, the task is to find the sum of the given infinite Arithmetic-Geometric Progression such that the absolute value of R is always less than 1.
Examples:
Input: A = 0, D = 1, R = 0.5
Output: 0.666667
Input: A = 2, D = 3, R = -0.3
Output: 0.549451
Approach: An arithmetic-geometric sequence is the result of the term-by-term multiplication of the geometric progression series with the corresponding terms of an arithmetic progression series. The series is given by:
a, (a + d) * r, (a + 2 * d) * r2, (a + 3 * d) * r3, …, [a + (N ? 1) * d] * r(N ? 1).
The Nth term of the Arithmetic-Geometric Progression is given by:
=> ![Rendered by QuickLaTeX.com T_N = [a + (N - 1) * d] * (b * r^{n - 1})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87b7f894daa8b072bc4ae02316a45992_l3.png)
The sum of the Arithmetic-Geometric Progression is given by:
=>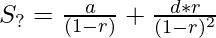
where, |r| < 1.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void sumOfInfiniteAGP(double a, double d,
double r)
{
double ans = a / (1 - r)
+ (d * r) / pow((1-r),2);
cout << ans;
}
int main()
{
double a = 0, d = 1, r = 0.5;
sumOfInfiniteAGP(a, d, r);
return 0;
}
|
Java
import java.lang.Math;
class GFG{
static void sumOfInfiniteAGP(double a, double d,
double r)
{
double ans = a / (1 - r) +
(d * r) / Math.pow((1-r),2);
System.out.print(ans);
}
public static void main(String[] args)
{
double a = 0, d = 1, r = 0.5;
sumOfInfiniteAGP(a, d, r);
}
}
|
Python3
def sumOfInfiniteAGP(a, d, r):
ans = a / (1 - r) + (d * r) / (1 - r)**2;
print (round(ans,6))
if __name__ == '__main__':
a, d, r = 0, 1, 0.5
sumOfInfiniteAGP(a, d, r)
|
C#
using System;
class GFG
{
static void sumOfInfiniteAGP(double a, double d,
double r)
{
double ans = a / (1 - r) + (d * r) / Math.Pow((1-r),2);
Console.Write(ans);
}
public static void Main()
{
double a = 0, d = 1, r = 0.5;
sumOfInfiniteAGP(a, d, r);
}
}
|
Javascript
<script>
function sumOfInfiniteAGP(a, d, r) {
let ans = a / (1 - r) +
(d * r) / Math.pow((1-r),2);
document.write(ans)
}
let a = 0, d = 1, r = 0.5;
sumOfInfiniteAGP(a, d, r);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...