Program to Calculate e^x by Recursion ( using Taylor Series )

The value of the Exponential function can be calculated using Taylor Series.

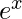 = 1 + x/1! + 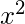/2! + 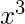/3! + ...... + until n terms

As the number of terms increases the more precise value of e^x is obtained.

To find e^x using the recursive function, we need to use static variables. A function can return only one value, and when we need to include multiple values in a recursive function, we use static variables. The Taylor Series is a combination of multiple values like sum, power and factorial term, hence we will use static variables.

For the power of x, we will use p, and for factorials, we will use f as static variables.

The function shown below is used to increase the power of x.

p = p*x

The function below is used to find factorials.

f = f*n

The function below is used to calculate the summation of the series.

r+p/f

Where r is the recursive call to the function.

Below is the implementation of the above idea.

C++

// C++ implementation of the approach
#include <iostream>
using namespace std;
 
// Recursive Function with static
// variables p and f
double e(int x, int n)
{
    static double p = 1, f = 1;
    double r;
 
    // Termination condition
    if (n == 0)
        return 1;
 
    // Recursive call
    r = e(x, n - 1);
 
    // Update the power of x
    p = p * x;
 
    // Factorial
    f = f * n;
 
    return (r + p / f);
}
 
// Driver code
int main()
{
    int x = 4, n = 15;
    cout<<"\n"<< e(x, n);
 
    return 0;
}
 
// this code is contributed by shivanisinghss2110

C

// C implementation of the approach
#include <stdio.h>
 
// Recursive Function with static
// variables p and f
double e(int x, int n)
{
    static double p = 1, f = 1;
    double r;
 
    // Termination condition
    if (n == 0)
        return 1;
 
    // Recursive call
    r = e(x, n - 1);
 
    // Update the power of x
    p = p * x;
 
    // Factorial
    f = f * n;
 
    return (r + p / f);
}
 
// Driver code
int main()
{
    int x = 4, n = 15;
    printf("%lf \n", e(x, n));
 
    return 0;
}

Java

// Java implementation of the approach
import java.text.*;
 
class GFG {
 
    // Recursive Function with static
    // variables p and f
    static double p = 1, f = 1;
    static double e(int x, int n)
    {
        double r;
 
        // Termination condition
        if (n == 0)
            return 1;
 
        // Recursive call
        r = e(x, n - 1);
 
        // Update the power of x
        p = p * x;
 
        // Factorial
        f = f * n;
 
        return (r + p / f);
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int x = 4, n = 15;
        DecimalFormat df = new DecimalFormat("0.######");
        System.out.println(df.format(e(x, n)));
    }
}
 
// This code is contributed by mits

Python3

# Python implementation of the approach
 
# Recursive Function
# global variables p and f
p = 1.0
f = 1.0
 
 
def e(x, n):
 
    global p, f
 
    # Termination condition
    if (n == 0):
        return 1
 
    # Recursive call
    r = e(x, n - 1)
 
    # Update the power of x
    p = p * x
 
    # Factorial
    f = f * n
 
    return (r + p / f)
 
# Driver code
 
 
x = 4
n = 15
print(e(x, n))
 
# This contributed by ihritik

C#

// C# implementation of the approach
using System;
 
class GFG {
 
    // Recursive Function with static
    // variables p and f
    static double p = 1, f = 1;
    static double e(int x, int n)
    {
        double r;
 
        // Termination condition
        if (n == 0)
            return 1;
 
        // Recursive call
        r = e(x, n - 1);
 
        // Update the power of x
        p = p * x;
 
        // Factorial
        f = f * n;
 
        return (r + p / f);
    }
 
    // Driver code
    static void Main()
    {
        int x = 4, n = 15;
        Console.WriteLine(Math.Round(e(x, n), 6));
    }
}
 
// This code is contributed by mits

Javascript

<script>
 
// Javascript implementation of the approach
 
// Recursive Function with static
// variables p and f
p = 1, f = 1;
function e(x, n)
{
    var r;
 
    // Termination condition
    if (n == 0)
        return 1;
 
    // Recursive call
    r = e(x, n - 1);
 
    // Update the power of x
    p = p * x;
 
    // Factorial
    f = f * n;
 
    return (r + p / f);
}
 
// Driver Code
var x = 4, n = 15;
var res = e(x, n);
 
document.write(res.toFixed(6));
 
// This code is contributed by kirti
 
</script>