Program to calculate distance between two points in 3 D
Last Updated :
20 Aug, 2022
Given two coordinates (x1, y1, z1) and (x2, y2, z2) in 3 dimension. The task is to find the distance between them.
Examples :
Input: x1, y1, z1 = (2, -5, 7)
x2, y2, z1 = (3, 4, 5)
Output: 9.2736184955
Input: x1, y1, z1 = (0, 0, 0)
x2, y2, z1 = (1, 1, 1)
Output: 1.73205080757
Approach: The formula for distance between two points in 3 dimension i.e (x1, y1, z1) and (x2, y2, z2) has been derived from Pythagorean theorem which is:
Distance = 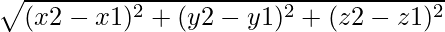
Below is the implementation of above formulae:
C++
#include <bits/stdc++.h>
#include <iomanip>
#include <iostream>
#include <math.h>
using namespace std;
void distance(float x1, float y1,
float z1, float x2,
float y2, float z2)
{
float d = sqrt(pow(x2 - x1, 2) +
pow(y2 - y1, 2) +
pow(z2 - z1, 2) * 1.0);
std::cout << std::fixed;
std::cout << std::setprecision(2);
cout << " Distance is " << d;
return;
}
int main()
{
float x1 = 2;
float y1 = -5;
float z1 = 7;
float x2 = 3;
float y2 = 4;
float z2 = 5;
distance(x1, y1, z1,
x2, y2, z2);
return 0;
}
|
C
#include <stdio.h>
#include<math.h>
void distance(float x1, float y1,
float z1, float x2,
float y2, float z2)
{
float d = sqrt(pow(x2 - x1, 2) +
pow(y2 - y1, 2) +
pow(z2 - z1, 2) * 1.0);
printf("Distance is %f", d);
return;
}
int main()
{
float x1 = 2;
float y1 = -5;
float z1 = 7;
float x2 = 3;
float y2 = 4;
float z2 = 5;
distance(x1, y1, z1,
x2, y2, z2);
return 0;
}
|
Java
import java .io.*;
import java.lang.Math;
class GFG
{
static void distance(float x1, float y1,
float z1, float x2,
float y2, float z2)
{
double d = Math.pow((Math.pow(x2 - x1, 2) +
Math.pow(y2 - y1, 2) +
Math.pow(z2 - z1, 2) *
1.0), 0.5);
System.out.println("Distance is "+ d);
return;
}
public static void main(String[] args)
{
float x1 = 2;
float y1 = -5;
float z1 = 7;
float x2 = 3;
float y2 = 4;
float z2 = 5;
distance(x1, y1, z1,
x2, y2, z2);
}
}
|
Python
import math
def distance(x1, y1, z1, x2, y2, z2):
d = math.sqrt(math.pow(x2 - x1, 2) +
math.pow(y2 - y1, 2) +
math.pow(z2 - z1, 2)* 1.0)
print("Distance is ")
print(d)
x1 = 2
y1 = -5
z1 = 7
x2 = 3
y2 = 4
z2 = 5
distance(x1, y1, z1, x2, y2, z2)
|
C#
using System;
class GFG
{
static void distance(float x1, float y1,
float z1, float x2,
float y2, float z2)
{
double d = Math.Pow((Math.Pow(x2 - x1, 2) +
Math.Pow(y2 - y1, 2) +
Math.Pow(z2 - z1, 2) *
1.0), 0.5);
Console.WriteLine("Distance is \n" + d);
return;
}
public static void Main()
{
float x1 = 2;
float y1 = -5;
float z1 = 7;
float x2 = 3;
float y2 = 4;
float z2 = 5;
distance(x1, y1, z1,
x2, y2, z2);
}
}
|
PHP
<?php
function distance($x1, $y1, $z1,
$x2, $y2, $z2)
{
$d = sqrt(pow($x2 - $x1, 2) +
pow($y2 - $y1, 2) +
pow($z2 - $z1, 2) * 1.0);
echo "Distance is ". $d;
}
$x1 = 2;
$y1 = -5;
$z1 = 7;
$x2 = 3;
$y2 = 4;
$z2 = 5;
distance($x1, $y1, $z1,
$x2, $y2, $z2);
?>
|
Javascript
<script>
function distance(x1 , y1 , z1 , x2 , y2 , z2) {
var d = Math.pow((Math.pow(x2 - x1, 2) +
Math.pow(y2 - y1, 2) +
Math.pow(z2 - z1, 2) * 1.0), 0.5);
document.write("Distance is " + d.toFixed(10));
return;
}
var x1 = 2;
var y1 = -5;
var z1 = 7;
var x2 = 3;
var y2 = 4;
var z2 = 5;
distance(x1, y1, z1, x2, y2, z2);
</script>
|
Output: Distance is
9.2736184955
Time complexity: O(logn) as the inbuilt pow and sqrt function takes logarithmic time to complete all the operations hence the overall time taken by the algorithm is logarithmic.
Auxiliary Space: O(1) since no extra array is used so the space taken by the algorithm is constant
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...