Program for Spearman’s Rank Correlation
Last Updated :
23 May, 2023
Prerequisite: Correlation Coefficient
Given two arrays X and Y. Find Spearman’s Rank Correlation. In Spearman rank correlation instead of working with the data values themselves (as discussed in Correlation coefficient), it works with the ranks of these values. The observations are first ranked and then these ranks are used in correlation. The Algorithm for this correlation is as follows
Rank each observation in X and store it in Rank_X
Rank each observation in Y and store it in Rank_Y
Obtain Pearson Correlation Coefficient for Rank_X and Rank_Y
The formula used to calculate Pearson’s Correlation Coefficient (r or rho) of sets X and Y is as follows:
![Rendered by QuickLaTeX.com {{\displaystyle r=\frac {n(\sum xy)-\left ( \sum x \right )\left ( \sum y \right )}{\sqrt{[n\sum x^2-(\sum x)^2 ][n\sum y^2 - (\sum y)^2]}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f14072313090dd1eef767a9045ec8d9_l3.png)
Algorithm for calculating Pearson’s Coefficient of Sets X and Y
function correlationCoefficient(X, Y)
n = X.size
sigma_x = sigma_y = sigma_xy = 0
sigma_xsq = sigma_ysq = 0
for i in 0...N-1
sigma_x = sigma_x + X[i]
sigma_y = sigma_y + Y[i]
sigma_xy = sigma_xy + X[i] * Y[i]
sigma_xsq = sigma_xsq + X[i] * X[i]
sigma_ysq = sigma_ysq + Y[i] * Y[i]
num =( n * sigma_xy - sigma_x * sigma_y)
den = sqrt( [n*sigma_xsq - (sigma_x)^ 2]*[ n*sigma_ysq - (sigma_y) ^ 2] )
return num/den
While assigning ranks, it may encounter ties i.e two or more observations having the same rank. To resolve ties, this will use fractional ranking scheme. In this scheme, if n observations have the same rank then each observation gets a fractional rank given by:
fractional_rank = (rank) + (n-1)/2
The next rank that gets assigned is rank + n and not rank + 1. For instance, if the 3 items have same rank r, then each gets fractional_rank as given above. The next rank that can be given to another observation is r + 3. Note that fractional ranks need not be fractions. They are the arithmetic mean of n consecutive ranks ex r, r + 1, r + 2 … r + n-1.
(r + r+1 + r+2 + ... + r+n-1) / n = r + (n-1)/2
Some Examples :
Input : X = [15 18 19 20 21]
Y = [25 26 28 27 29]
Solution : Rank_X = [1 2 3 4 5]
Rank_Y = [1 2 4 3 5 ]
sigma_x = 1+2+3+4+5 = 15
sigma_y = 1+2+4+3+5 = 15
sigma_xy = 1*2+2*2+3*4+4*3+5*5 = 54
sigma_xsq = 1*1+2*2+3*3+4*4+5*5 = 55
sigma_ysq = 1*1+2*2+3*3+4*4+5*5 = 55
Substitute values in formula
Coefficient = Pearson(Rank_X, Rank_Y) = 0.9
Input: X = [15 18 21 15 21 ]
Y = [25 25 27 27 27 ]
Solution: Rank_X = [1.5 3 4.5 1.5 4.5]
Rank_Y = [1.5 1.5 4 4 4]
Calculate and substitute values of sigma_x, sigma_y,
sigma_xy, sigma_xsq, sigma_ysq.
Coefficient = Pearson(Rank_X, Rank_Y) = 0.456435
The Algorithm for fractional ranking scheme is given below:
function rankify(X)
N = X.size()
// Vector to store ranks
Rank_X(N)
for i = 0 ... N-1
r = 1 and s = 1
// Count no of smaller elements in 0...i-1
for j = 0...i-1
if X[j] < X[i]
r = r+1
if X[j] == X[i]
s = s+1
// Count no of smaller elements in i+1...N-1
for j = i+1...N-1
if X[j] < X[i]
r = r+1
if X[j] == X[i]
s = s+1
//Assign Fractional Rank
Rank_X[i] = r + (s-1) * 0.5
return Rank_X
Note:
There is a direct formula to calculate Spearman’s coefficient given by 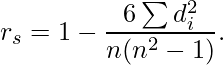 However, we need to put in a correction term to resolve each tie and hence this formula has not been discussed. Calculating Spearman’s coefficient from the correlation coefficient of ranks is the most general method.
However, we need to put in a correction term to resolve each tie and hence this formula has not been discussed. Calculating Spearman’s coefficient from the correlation coefficient of ranks is the most general method.
A CPP Program to evaluate Spearman’s coefficient is given below
C++
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef vector<float> Vector;
void printVector(const Vector &X)
{
for (auto i: X)
cout << i << " ";
cout << endl;
}
Vector rankify(Vector & X) {
int N = X.size();
Vector Rank_X(N);
for(int i = 0; i < N; i++)
{
int r = 1, s = 1;
for(int j = 0; j < i; j++) {
if (X[j] < X[i] ) r++;
if (X[j] == X[i] ) s++;
}
for (int j = i+1; j < N; j++) {
if (X[j] < X[i] ) r++;
if (X[j] == X[i] ) s++;
}
Rank_X[i] = r + (s-1) * 0.5;
}
return Rank_X;
}
float correlationCoefficient
(Vector &X, Vector &Y)
{
int n = X.size();
float sum_X = 0, sum_Y = 0,
sum_XY = 0;
float squareSum_X = 0,
squareSum_Y = 0;
for (int i = 0; i < n; i++)
{
sum_X = sum_X + X[i];
sum_Y = sum_Y + Y[i];
sum_XY = sum_XY + X[i] * Y[i];
squareSum_X = squareSum_X +
X[i] * X[i];
squareSum_Y = squareSum_Y +
Y[i] * Y[i];
}
float corr = (float)(n * sum_XY -
sum_X * sum_Y) /
sqrt((n * squareSum_X -
sum_X * sum_X) *
(n * squareSum_Y -
sum_Y * sum_Y));
return corr;
}
int main()
{
Vector X = {15,18,21, 15, 21};
Vector Y= {25,25,27,27,27};
Vector rank_x = rankify(X);
Vector rank_y = rankify(Y);
cout << "Vector X" << endl;
printVector(X);
cout << "Rankings of X" << endl;
printVector(rank_x);
cout << "Vector Y" << endl;
printVector(Y);
cout << "Rankings of Y" << endl;
printVector(rank_y);
cout << "Spearman's Rank correlation: "
<< endl;
cout<<correlationCoefficient(rank_x,
rank_y);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void printVector(ArrayList<Double> X)
{
for (double i : X)
System.out.print(i + " ");
System.out.println();
}
static ArrayList<Double> rankify(ArrayList<Double> X)
{
int N = X.size();
ArrayList<Double> Rank_X = new ArrayList<Double>();
for (int i = 0; i < N; i++) {
Rank_X.add(0d);
int r = 1, s = 1;
for (int j = 0; j < i; j++) {
if (X.get(j) < X.get(i))
r++;
if (X.get(j) == X.get(i))
s++;
}
for (int j = i + 1; j < N; j++) {
if (X.get(j) < X.get(i))
r++;
if (X.get(j) == X.get(i))
s++;
}
Rank_X.set(i, (r + (s - 1) * 0.5));
}
return Rank_X;
}
static double
correlationCoefficient(ArrayList<Double> X,
ArrayList<Double> Y)
{
int n = X.size();
double sum_X = 0, sum_Y = 0, sum_XY = 0;
double squareSum_X = 0, squareSum_Y = 0;
for (int i = 0; i < n; i++) {
sum_X = sum_X + X.get(i);
sum_Y = sum_Y + Y.get(i);
sum_XY = sum_XY + X.get(i) * Y.get(i);
squareSum_X = squareSum_X + X.get(i) * X.get(i);
squareSum_Y = squareSum_Y + Y.get(i) * Y.get(i);
}
double corr
= (n * sum_XY - sum_X * sum_Y)
/ Math.sqrt(
(n * squareSum_X - sum_X * sum_X)
* (n * squareSum_Y - sum_Y * sum_Y));
return corr;
}
public static void main(String[] args)
{
ArrayList<Double> X = new ArrayList<Double>(
Arrays.asList(15d, 18d, 21d, 15d, 21d));
ArrayList<Double> Y = new ArrayList<Double>(
Arrays.asList(25d, 25d, 27d, 27d, 27d));
ArrayList<Double> rank_x = rankify(X);
ArrayList<Double> rank_y = rankify(Y);
System.out.println("Vector X");
printVector(X);
System.out.println("Rankings of X");
printVector(rank_x);
System.out.println("Vector Y");
printVector(Y);
System.out.println("Rankings of Y");
printVector(rank_y);
System.out.println("Spearman's Rank correlation: ");
System.out.println(
correlationCoefficient(rank_x, rank_y));
}
}
|
Python3
def printVector(X):
print(*X)
def rankify(X):
N = len(X)
Rank_X = [None for _ in range(N)]
for i in range(N):
r = 1
s = 1
for j in range(i):
if (X[j] < X[i]):
r += 1
if (X[j] == X[i]):
s += 1
for j in range(i+1, N):
if (X[j] < X[i]):
r += 1
if (X[j] == X[i]):
s += 1
Rank_X[i] = r + (s-1) * 0.5
return Rank_X
def correlationCoefficient(X, Y):
n = len(X)
sum_X = 0
sum_Y = 0
sum_XY = 0
squareSum_X = 0
squareSum_Y = 0
for i in range(n):
sum_X = sum_X + X[i]
sum_Y = sum_Y + Y[i]
sum_XY = sum_XY + X[i] * Y[i]
squareSum_X = squareSum_X + X[i] * X[i]
squareSum_Y = squareSum_Y + Y[i] * Y[i]
corr = (n * sum_XY - sum_X * sum_Y) / ((n * squareSum_X -
sum_X * sum_X) * (n * squareSum_Y - sum_Y * sum_Y)) ** 0.5
return corr
X = [15, 18, 21, 15, 21]
Y = [25, 25, 27, 27, 27]
rank_x = rankify(X)
rank_y = rankify(Y)
print("Vector X")
printVector(X)
print("Rankings of X")
printVector(rank_x)
print("Vector Y")
printVector(Y)
print("Rankings of Y")
printVector(rank_y)
print("Spearman's Rank correlation: ")
print(correlationCoefficient(rank_x, rank_y))
|
C#
using System;
using System.Collections.Generic;
class GFG {
static void printVector(List<double> X)
{
foreach(var i in X) Console.Write(i + " ");
Console.WriteLine();
}
static List<double> rankify(List<double> X)
{
int N = X.Count;
List<double> Rank_X = new List<double>();
for (int i = 0; i < N; i++) {
Rank_X.Add(0);
int r = 1, s = 1;
for (int j = 0; j < i; j++) {
if (X[j] < X[i])
r++;
if (X[j] == X[i])
s++;
}
for (int j = i + 1; j < N; j++) {
if (X[j] < X[i])
r++;
if (X[j] == X[i])
s++;
}
Rank_X[i] = (r + (s - 1) * 0.5);
}
return Rank_X;
}
static double correlationCoefficient(List<double> X,
List<double> Y)
{
int n = X.Count;
double sum_X = 0, sum_Y = 0, sum_XY = 0;
double squareSum_X = 0, squareSum_Y = 0;
for (int i = 0; i < n; i++) {
sum_X = sum_X + X[i];
sum_Y = sum_Y + Y[i];
sum_XY = sum_XY + X[i] * Y[i];
squareSum_X = squareSum_X + X[i] * X[i];
squareSum_Y = squareSum_Y + Y[i] * Y[i];
}
double corr
= (n * sum_XY - sum_X * sum_Y)
/ Math.Sqrt(
(n * squareSum_X - sum_X * sum_X)
* (n * squareSum_Y - sum_Y * sum_Y));
return corr;
}
public static void Main(string[] args)
{
List<double> X = new List<double>(
new double[] { 15, 18, 21, 15, 21 });
List<double> Y = new List<double>(
new double[] { 25, 25, 27, 27, 27 });
List<double> rank_x = rankify(X);
List<double> rank_y = rankify(Y);
Console.WriteLine("Vector X");
printVector(X);
Console.WriteLine("Rankings of X");
printVector(rank_x);
Console.WriteLine("Vector Y");
printVector(Y);
Console.WriteLine("Rankings of Y");
printVector(rank_y);
Console.WriteLine("Spearman's Rank correlation: ");
Console.WriteLine(
correlationCoefficient(rank_x, rank_y));
}
}
|
Javascript
function printVector(X)
{
for (var i of X)
process.stdout.write(i + " ");
process.stdout.write("\n");
}
function rankify(X) {
let N = X.length;
let Rank_X = new Array(N);
for(var i = 0; i < N; i++)
{
var r = 1, s = 1;
for(var j = 0; j < i; j++) {
if (X[j] < X[i] ) r++;
if (X[j] == X[i] ) s++;
}
for (var j = i+1; j < N; j++) {
if (X[j] < X[i] ) r++;
if (X[j] == X[i] ) s++;
}
Rank_X[i] = r + (s-1) * 0.5;
}
return Rank_X;
}
function correlationCoefficient
(X, Y)
{
let n = X.length;
let sum_X = 0, sum_Y = 0,
sum_XY = 0;
let squareSum_X = 0,
squareSum_Y = 0;
for (var i = 0; i < n; i++)
{
sum_X = sum_X + X[i];
sum_Y = sum_Y + Y[i];
sum_XY = sum_XY + X[i] * Y[i];
squareSum_X = squareSum_X +
X[i] * X[i];
squareSum_Y = squareSum_Y +
Y[i] * Y[i];
}
let corr = (n * sum_XY -
sum_X * sum_Y) /
Math.sqrt((n * squareSum_X -
sum_X * sum_X) *
(n * squareSum_Y -
sum_Y * sum_Y));
return corr;
}
let X = [15,18,21, 15, 21];
let Y= [25,25,27,27,27];
let rank_x = rankify(X);
let rank_y = rankify(Y);
console.log("Vector X");
printVector(X);
console.log("Rankings of X");
printVector(rank_x);
console.log("Vector Y");
printVector(Y);
console.log("Rankings of Y");
printVector(rank_y);
console.log("Spearman's Rank correlation: ");
console.log(correlationCoefficient(rank_x,
rank_y));
|
OutputVector X
15 18 21 15 21
Rankings of X
1.5 3 4.5 1.5 4.5
Vector Y
25 25 27 27 27
Rankings of Y
1.5 1.5 4 4 4
Spearman's Rank correlation:
0.456435
Time Complexity: O(N*N)
Auxiliary Space: O(N)
Python code to calculate Spearman’s Correlation using Scipy Library
We can use scipy to calculate Spearman’s correlation coefficient. Scipy is one of the most used python library for mathematical calculations.
Python3
from scipy.stats import spearmanr
x = [1, 2, 3, 4, 5]
y = [5, 4, 3, 2, 1]
corr, pval = spearmanr(x, y)
print("Spearman's correlation coefficient:", corr)
print("p-value:", pval)
|
Output:
Spearman's correlation coefficient: -0.9999999999999999
p-value: 1.4042654220543672e-24
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...