Program for Perrin numbers
Last Updated :
14 Jul, 2022
The Perrin numbers are the numbers in the following integer sequence.
3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39 …
In mathematical terms, the sequence p(n) of Perrin numbers is defined by the recurrence relation
P(n) = P(n-2) + P(n-3) for n > 2,
with initial values
P(0) = 3, P(1) = 0, P(2) = 2.
Write a function int per(int n) that returns p(n). For example, if n = 0, then per() should return 3. If n = 1, then it should return 0 If n = 2, then it should return 2. For n > 2, it should return p(n-2) + p(n-3)
Method 1 ( Use recursion : Exponential )
Below is simple recursive implementation of above formula.
C++
#include <bits/stdc++.h>
using namespace std;
int per(int n)
{
if (n == 0)
return 3;
if (n == 1)
return 0;
if (n == 2)
return 2;
return per(n - 2) + per(n - 3);
}
int main()
{
int n = 9;
cout << per(n);
return 0;
}
|
C
#include <stdio.h>
int per(int n)
{
if (n == 0)
return 3;
if (n == 1)
return 0;
if (n == 2)
return 2;
return per(n - 2) + per(n - 3);
}
int main()
{
int n = 9;
printf("%d", per(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int per(int n)
{
if (n == 0)
return 3;
if (n == 1)
return 0;
if (n == 2)
return 2;
return per(n - 2) + per(n - 3);
}
public static void main(String[] args)
{
int n = 9;
System.out.println(per(n));
}
}
|
Python3
def per(n):
if (n == 0):
return 3;
if (n == 1):
return 0;
if (n == 2):
return 2;
return per(n - 2) + per(n - 3);
n = 9;
print(per(n));
|
C#
using System;
class GFG {
static int per(int n)
{
if (n == 0)
return 3;
if (n == 1)
return 0;
if (n == 2)
return 2;
return per(n - 2) + per(n - 3);
}
public static void Main()
{
int n = 9;
Console.Write(per(n));
}
}
|
PHP
<?php
function per($n)
{
if ($n == 0)
return 3;
if ($n == 1)
return 0;
if ($n == 2)
return 2;
return per($n - 2) +
per($n - 3);
}
$n = 9;
echo per($n);
#This code is contributed ajit.
?>
|
Javascript
<script>
function per(n)
{
if (n == 0)
return 3;
if (n == 1)
return 0;
if (n == 2)
return 2;
return per(n - 2) + per(n - 3);
}
let n = 9;
document.write(per(n));
</script>
|
Output:
12
We see that in this implementation a lot of repeated work in the following recursion tree.
per(8)
/ \
per(6) per(5)
/ \ / \
per(4) per(3) per(3) per(2)
/ \ / \ / \
per(2) per(1) per(1) per(0) per(1) per(0)
Method 2: ( Optimized : Linear)
C++
#include <bits/stdc++.h>
using namespace std;
int per(int n)
{
int a = 3, b = 0, c = 2, i;
int m;
if (n == 0)
return a;
if (n == 1)
return b;
if (n == 2)
return c;
while (n > 2) {
m = a + b;
a = b;
b = c;
c = m;
n--;
}
return m;
}
int main()
{
int n = 9;
cout << per(n);
return 0;
}
|
C
#include <stdio.h>
int per(int n)
{
int a = 3, b = 0, c = 2, i;
int m;
if (n == 0)
return a;
if (n == 1)
return b;
if (n == 2)
return c;
while (n > 2) {
m = a + b;
a = b;
b = c;
c = m;
n--;
}
return m;
}
int main()
{
int n = 9;
printf("%d", per(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int per(int n)
{
int a = 3, b = 0, c = 2, i;
int m = 0;
if (n == 0)
return a;
if (n == 1)
return b;
if (n == 2)
return c;
while (n > 2) {
m = a + b;
a = b;
b = c;
c = m;
n--;
}
return m;
}
public static void main(String[] args)
{
int n = 9;
System.out.println(per(n));
}
}
|
Python3
def per(n):
a = 3;
b = 0;
c = 2;
if (n == 0):
return a;
if (n == 1):
return b;
if (n == 2):
return c;
while (n > 2):
m = a + b;
a = b;
b = c;
c = m;
n -= 1
return m
n = 9;
print(per(n));
|
C#
using System;
class GFG {
static int per(int n)
{
int a = 3, b = 0, c = 2;
int m = 0;
if (n == 0)
return a;
if (n == 1)
return b;
if (n == 2)
return c;
while (n > 2) {
m = a + b;
a = b;
b = c;
c = m;
n--;
}
return m;
}
public static void Main()
{
int n = 9;
Console.WriteLine(per(n));
}
}
|
PHP
<?php
function per($n)
{
$a = 3; $b = 0;
$c = 2; $i;
$m;
if ($n == 0)
return $a;
if ($n == 1)
return $b;
if ($n == 2)
return $c;
while ($n > 2)
{
$m = $a + $b;
$a = $b;
$b = $c;
$c = $m;
$n--;
}
return $m;
}
$n = 9;
echo per($n);
?>
|
Javascript
<script>
function per(n)
{
let a = 3;
let b = 0;
let c = 2;
let i;
let m;
if (n == 0)
return a;
if (n == 1)
return b;
if (n == 2)
return c;
while (n > 2)
{
m = a + b;
a = b;
b = c;
c = m;
n--;
}
return m;
}
n = 9;
document.write(per(n));
</script>
|
Output:
12
Time Complexity : O(n)
Auxiliary Space : O(1)
Method 3: (Further Optimized : Logarithmic)
We can further optimize using Matrix Exponentiation. The matrix power formula for n’th Perrin number is
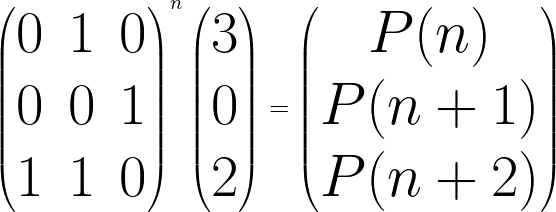
We can implement this method similar to implementation of method 5 of Fibonacci numbers. Since we can compute n’th power of a constant matrix in O(Log n), time complexity of this method is O(Log n)
Application :
The number of different maximal independent sets in an n-vertex cycle graph is counted by the nth Perrin number for n > 1
Related Article :
Sum of Perrin Numbers
Reference:
https://en.wikipedia.org/wiki/Perrin_number
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...