Program for finding the Integral of a given function using Boole’s Rule

Last Updated : 18 Sep, 2022

Given a function, f(x), tabulated at points

$x_i$

equally spaced by

$h=x_{i+1} - x_i$

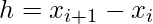
such that

$f_1 = f(x_1)$ [Tex]f_2=f(x_2)[/Tex]

…..and so on

The upper and lower limits a, b correspond to which the integral needs to be found, the task is to find the integral value of the given equation f(x).
Examples:

Input: a = 0, b = 4,

$f(x)= \frac{1}{1+x}$

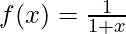
Output: 1.6178
Explanation:
Integral of (1 / (1 + x)) is ⁴ln(|1 + x|)₀ + c.
On substituting the limits, ln(|5|) + ln(|1|) = 1.6178.
Input: a = 0.2, b = 0.6,

$f(x)= \frac{1}{x^2}$

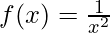
Output: 0.3430

Approach: In this article, Boole’s rule is discussed to compute the approximate integral value of the given function f(x).
Boole’s rule is a numerical integration technique to find the approximate value of the integral. It is named after a largely self-taught mathematician, philosopher, and logician George Boole. The idea of the Boole’s technique is to approximate the integral using the values of ‘f_k‘ at some equally spaced values(h in the given image). The following illustration shows how various f_k’s are considered:

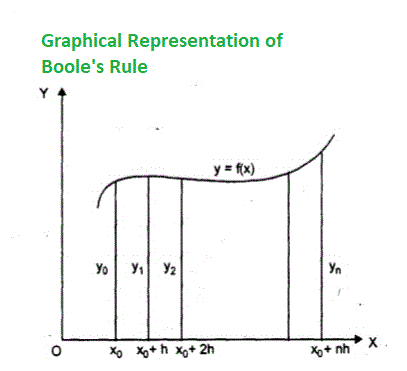
The integral value of Boole’s rule is given by the formula:

$\int_{x_{1}}^{x_{5}} f(x)dx = \frac{2}{45}h(7f_{1} + 32f_{2} + 12f_{3} + 32f_{4} + 7f_{5}) + \text{Error term}$

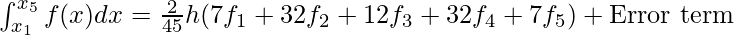
In the above formula, an error term which comes when integration is of order 6. The error term is

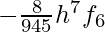$- \frac{8}{945}h^{7}f_{6}$ [Tex]f_1, f_2, f_3, f_4, f_5, [/Tex]

Are the values of f(x) at their respective intervals of x.
Therefore, the following steps can be followed to compute the integral of some function f(x) in the interval (a, b):
1. The value of n=6, which is the number of parts the interval is divided into.
2. Calculate the width, h = (b – a)/4.
3. Calculate the values of x₁ to x₅ as

$x_1 = a, x_2 = x_1 + h, x_3 = x_1 + 2h, ...x_5=x_1 +4h$

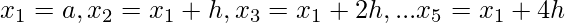
Consider y = f(x). Now find the values

$y(y_1, y_2, .. y_5)$

for the corresponding

$x(x_1, x_2, x_3... x_5)$

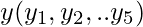
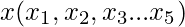
values.
Substitute all the values in Boole’s rule to calculate the integral value.

Below is the implementation of the above approach:

C++

// C++ program to implement Boole's Rule
// on the given function
#include <bits/stdc++.h>
using namespace std;
 
// In order to represent the implementation,
// a function f(x) = 1/(1 + x) is considered
// in this program
 
// Function to return the value of f(x)
// for the given value of x
float y(float x)
{
    return (1 / (1 + x));
}
 
// Function to computes the integrand of y
// at the given intervals of x with
// step size h and the initial limit a
// and final limit b
float BooleRule(float a, float b)
{
 
    // Number of intervals
    int n = 4;
    int h;
 
    // Computing the step size
    h = ((b - a) / n);
    float sum = 0;
 
    // Substituing a = 0, b = 4 and h = 1
    float bl = ((7 * y(a) + 
                32 * y(a + h) +
                12 * y(a + 2 * h) + 
                32 * y(a + 3 * h) + 
                 7 * y(a + 4 * h)) *
                 2 * h / 45);
 
    sum = sum + bl;
    return sum;
}
 
// Driver code
int main()
{
    float lowlimit = 0;
    float upplimit = 4;
     
    cout << fixed << setprecision(4) << 
        "f(x) = " << BooleRule(0, 4);
         
    return 0;
}
 
// This code is contributed by shivanisinghss2110

C

// C program to implement Boole's Rule
// on the given function
 
#include <math.h>
#include <stdio.h>
 
// In order to represent the implementation,
// a function f(x) = 1/(1 + x) is considered
// in this program
 
// Function to return the value of f(x)
// for the given value of x
float y(float x)
{
    return (1 / (1 + x));
}
 
// Function to computes the integrand of y
// at the given intervals of x with
// step size h and the initial limit a
// and final limit b
float BooleRule(float a, float b)
{
    // Number of intervals
 
    int n = 4;
    int h;
 
    // Computing the step size
    h = ((b - a) / n);
    float sum = 0;
 
    // Substituing a = 0, b = 4 and h = 1
    float bl = (7 * y(a) + 32 * y(a + h)
                + 12 * y(a + 2 * h)
                + 32 * y(a + 3 * h)
                + 7 * y(a + 4 * h))
               * 2 * h / 45;
 
    sum = sum + bl;
    return sum;
}
 
// Driver code
int main()
{
    float lowlimit = 0;
    float upplimit = 4;
    printf("f(x) = %.4f",
           BooleRule(0, 4));
    return 0;
}

Java

// Java program to implement Boole's Rule
// on the given function
class GFG{
     
// In order to represent the implementation,
// a function f(x) = 1/(1 + x) is considered
// in this program
  
// Function to return the value of f(x)
// for the given value of x
static float y(float x)
{
    return (1 / (1 + x));
}
  
// Function to computes the integrand of y
// at the given intervals of x with
// step size h and the initial limit a
// and final limit b
static float BooleRule(float a, float b)
{
    // Number of intervals
  
    int n = 4;
    int h;
  
    // Computing the step size
    h = (int) ((b - a) / n);
    float sum = 0;
  
    // Substituing a = 0, b = 4 and h = 1
    float bl = (7 * y(a) + 32 * y(a + h)
                + 12 * y(a + 2 * h)
                + 32 * y(a + 3 * h)
                + 7 * y(a + 4 * h))
               * 2 * h / 45;
  
    sum = sum + bl;
    return sum;
}
  
// Driver code
public static void main(String[] args)
{
    System.out.printf(("f(x) = %.4f"),
           BooleRule(0, 4));
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 program to implement Boole's Rule
# on the given function
 
# In order to represent the implementation,
# a function f(x) = 1/(1 + x) is considered
# in this program
 
# Function to return the value of f(x)
# for the given value of x
def y(x):
    return (1 / (1 + x))
 
# Function to computes the integrand of y
# at the given intervals of x with
# step size h and the initial limit a
# and final limit b
def BooleRule(a, b):
     
    # Number of intervals
    n = 4
 
    # Computing the step size
    h = ((b - a) / n)
    sum = 0
 
    # Substituing a = 0, b = 4 and h = 1
    bl = (7 * y(a) + 32 * y(a + h) + 12 *
        y(a + 2 * h)+32 * y(a + 3 * h)+7 *
        y(a + 4 * h))* 2 * h / 45
 
    sum = sum + bl
    return sum
 
# Driver code
if __name__ == '__main__':
    lowlimit = 0
    upplimit = 4
    print("f(x) =",round(BooleRule(0, 4),4))
 
# This code is contributed by Surendra_Gangwar

C#

// C# program to implement Boole's
// Rule on the given function
using System;
class GFG{
 
// In order to represent the 
// implementation, a function 
// f(x) = 1/(1 + x) is considered 
// in this program
 
// Function to return the value of
// f(x) for the given value of x
static float y(float x) 
{ 
  return (1 / (1 + x)); 
}
 
// Function to computes the integrand
// of y at the given intervals of x 
// with step size h and the initial 
// limit a and final limit b
static float BooleRule(float a, 
                       float b)
{
  // Number of intervals
  int n = 4;
  int h;
 
  // Computing the step size
  h = (int)((b - a) / n);
  float sum = 0;
 
  // Substituing a = 0, b = 4 
  // and h = 1
  float bl = (7 * y(a) + 32 * 
              y(a + h) + 12 * 
              y(a + 2 * h) + 
              32 * y(a + 3 * 
              h) + 7 * y(a + 
              4 * h)) * 2 *  
              h / 45;
 
  sum = sum + bl;
  return sum;
}
 
// Driver code
public static void Main(string[] args)
{
  Console.Write(("f(x) = " + 
                  System.Math.Round(
                  BooleRule(0, 4), 4)));
}
}
 
// This code is contributed by Chitranayal

Javascript

<script>
 
// JavaScript program to implement Boole's Rule
// on the given function
 
// In order to represent the implementation,
// a function f(x) = 1/(1 + x) is considered
// in this program
   
// Function to return the value of f(x)
// for the given value of x
function y(x)
{
    return (1 / (1 + x));
}
   
// Function to computes the integrand of y
// at the given intervals of x with
// step size h and the initial limit a
// and final limit b
function BooleRule(a, b)
{
    // Number of intervals
   
    let n = 4;
    let h;
   
    // Computing the step size
    h =  ((b - a) / n);
    let sum = 0;
   
    // Substituing a = 0, b = 4 and h = 1
    let bl = (7 * y(a) + 32 * y(a + h)
                + 12 * y(a + 2 * h)
                + 32 * y(a + 3 * h)
                + 7 * y(a + 4 * h))
               * 2 * h / 45;
   
    sum = sum + bl;
    return sum;
}
 
// Driver Code
     
    document.write("f(x) = " +
    BooleRule(0, 4).toFixed(4));
            
</script>

Output:

f(x) = 1.6178

Time Complexity: O(1)

Auxiliary Space: O(1)

Suggest improvement

Program to check if N is a Centered Tridecagonal Number

Count rotations which are divisible by 10

Share your thoughts in the comments

Program for finding the Integral of a given function using Boole’s Rule

C++

C

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?