Program to find area of a Circular Segment
Last Updated :
20 Feb, 2023
In a circle, if a chord is drawn then that chord divides the whole circle into two parts. These two parts of the circle are called segments of the circle. The smaller area is known as the Minor segment and the larger area is called as the Major segment.
In the figure below, the chord AB divides the circle into minor and major segments.

We are given radius of circle and angle that forms minor segment. We need to find areas of two segments.
Examples :
Input :
radius = 21.0
angle = 120.0
Output :
Area of minor segment 270.855
Area of major segment 1114.59
Input :
radius = 10.0
angle = 90.0
Output :
Area of minor segment 28.5397
Area of major segment 285.619
Area of the segment :
For that, we join the end points of the chord with the center of the circle resulting in a sector which subtends some ‘angle’ at the center. And a perpendicular is drawn from the center of the circle on the chord AB. By congruence of triangles, we obtain that the ? AOP = ? BOP = 1/2(angle).
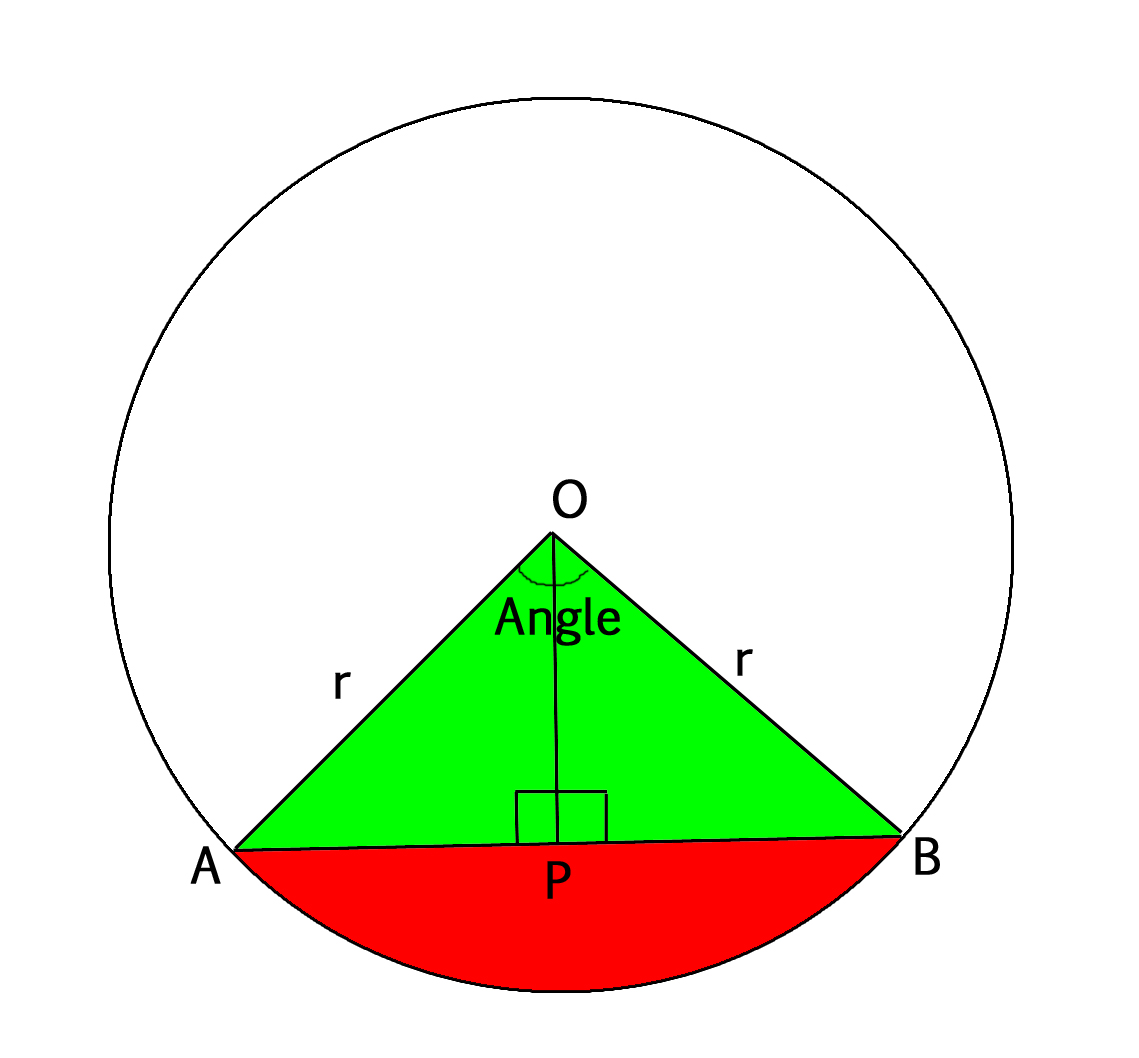
Formula for Area of Segment :
Area of Segment = Area of sector - Area of Triangle OAB
= pi * r2 * (angle/360) -
Area of Triangle OAB
For detailed information about formula of Area of Sector, refer https://www.geeksforgeeks.org/area-of-a-sector/.

In the figure above, assume angle made by sector = X,
so ? AOP = ? BOP = X/2
Area of Triangle AOB = 1/2 * base * height
= 1/2 * AB * OP
Now in Triangle AOP, By trigonometry
Cos(X/2) = OP/AO i.e. OP = AO * Cos(X/2)
OP = r * Cos(X/2)
Sin(X/2) = AP/AO i.e. AP = AO * Sin(X/2)
AP = r * Sin(X/2)
So,
Base = AB = AP + PB
= 2 * AP
= 2 * r * Sin(X/2)
Height = OP = r * Cos(X/2)
Area of triangle = 1/2 * (2 * r * Sin(X/2)) * (r * Cos(X/2))
= 1/2 * r2 * Sin(X)
[Using identity 2 * Sin(A) * Cos(A)]
= Sin(2 * A))
Hence Area of Segment = pi * r2 * (angle/360) - 1/2 * r2 * Sin(angle)
C++
#include <bits/stdc++.h>
using namespace std;
float pi = 3.14159;
float area_of_segment(float radius,
float angle)
{
float area_of_sector = pi *
(radius * radius)
*(angle / 360);
float area_of_triangle = (float)1 / 2 *
(radius * radius) *
sin((angle * pi) / 180);
return area_of_sector - area_of_triangle;
}
int main()
{
float radius = 10.0, angle = 90.0;
cout << "Area of minor segment = "
<< area_of_segment(radius, angle) << endl;
cout << "Area of major segment = "
<< area_of_segment(radius, (360 - angle));
}
|
Java
class GFG {
static float pi = 3.14159f;
static float area_of_segment(float radius,
float angle)
{
float area_of_sector = pi *
(radius * radius) * (angle / 360);
float area_of_triangle =
(float)1 / 2 * (radius * radius) *
(float)Math.sin((angle * pi) / 180);
return area_of_sector - area_of_triangle;
}
public static void main(String[] args)
{
float radius = 10.0f, angle = 90.0f;
System.out.println("Area of minor segment = " +
area_of_segment(radius, angle));
System.out.println("Area of major segment = " +
area_of_segment(radius, (360 - angle)));
}
}
|
Python
import math
pi = 3.14159
def area_of_segment(radius, angle):
area_of_sector = pi *
(radius * radius)
* (angle / 360)
area_of_triangle = 1 / 2 *
(radius * radius) *
math.sin((angle * pi) / 180)
return area_of_sector - area_of_triangle;
radius = 10.0
angle = 90.0
print("Area of minor segment =",
area_of_segment(radius, angle))
print("Area of major segment =",
area_of_segment(radius, (360 - angle)))
|
C#
using System;
class GFG {
static float pi = 3.14159f;
static float area_of_segment(float radius,
float angle)
{
float area_of_sector = pi * (radius * radius)
* (angle / 360);
float area_of_triangle =(float)1 / 2 * (radius * radius)
*(float)Math.Sin((angle * pi) / 180);
return area_of_sector - area_of_triangle;
}
public static void Main()
{
float radius = 10.0f, angle = 90.0f;
Console.WriteLine("Area of minor segment = " +
area_of_segment(radius, angle));
Console.WriteLine("Area of major segment = " +
area_of_segment(radius, (360 - angle)));
}
}
|
PHP
<?php
function area_of_segment($radius,
$angle)
{
$pi = 3.14159;
$area_of_sector = $pi * ($radius * $radius) *
($angle / 360);
$area_of_triangle = 1 / 2 * ($radius * $radius)
* sin(($angle * $pi) / 180);
return $area_of_sector - $area_of_triangle;
}
$radius = 10.0;
$angle = 90.0;
echo ("Area of minor segment = ");
echo( area_of_segment($radius, $angle));
echo("\n");
echo("Area of major segment = ");
echo(area_of_segment($radius, (360 - $angle)));
?>
|
Javascript
<script>
let pi = 3.14159;
function area_of_segment(radius,
angle)
{
let area_of_sector = pi *
(radius * radius) * (angle / 360);
let area_of_triangle =
1 / 2 * (radius * radius) *
Math.sin((angle * pi) / 180);
return area_of_sector - area_of_triangle;
}
let radius = 10.0, angle = 90.0;
document.write("Area of minor segment = " +
area_of_segment(radius, angle) + "<br/>");
document.write("Area of major segment = " +
area_of_segment(radius, (360 - angle)));
</script>
|
Output :
Area of minor segment = 28.5397
Area of major segment = 285.619
Time Complexity: O(1)
Auxiliary Space: O(1)
Please suggest if someone has a better solution which is more efficient in terms of space and time.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...