Product of N terms of a given Geometric series
Last Updated :
23 Sep, 2022
Given a number N, the first term ‘a’ and a common ratio ‘r’ of a Geometric Progression, the task is to find the product of first N terms of the given Geometric Progression.
Examples:
Input: a = 1, r = 2, N = 4
Output: 64
Explanation:
First four term for the above G.P. is 1, 2, 4, 8.
Product of four numbers is 1*2*4*8 = 64
Input: a = 1, r = 0.5, N = 3
Output: 0.125
Explanation:
First three term for the above G.P. is 1, 1/2, 1/4.
Product of four numbers is 1*(1/2)*(1/4) = 1/8 = 0.125
Naive Approach: The idea is to find all the N terms of the given geometric progression and multiply all the terms obtained.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float productOfGP(float a, float r, int n)
{
float product = 1;
for (int i = 0; i < n; i++) {
product = product * a;
a = a * r;
}
return product;
}
int main()
{
float a = 1, r = 2;
int N = 4;
cout << productOfGP(a, r, N);
}
|
Java
import java.util.*;
class GFG{
static float productOfGP(float a,
float r, int n)
{
float product = 1;
for (int i = 0; i < n; i++)
{
product = product * a;
a = a * r;
}
return product;
}
public static void main(String args[])
{
float a = 1, r = 2;
int N = 4;
System.out.print(productOfGP(a, r, N));
}
}
|
Python3
def productOfGP(a, r, n):
product = 1;
for i in range(0, n):
product = product * a;
a = a * r;
return product;
a = 1
r = 2;
N = 4;
print(productOfGP(a, r, N))
|
C#
using System;
class GFG{
static float productOfGP(float a,
float r, int n)
{
float product = 1;
for (int i = 0; i < n; i++)
{
product = product * a;
a = a * r;
}
return product;
}
public static void Main()
{
float a = 1, r = 2;
int N = 4;
Console.Write(productOfGP(a, r, N));
}
}
|
Javascript
<script>
function productOfGP(a, r, n)
{
let product = 1;
for (let i = 0; i < n; i++)
{
product = product * a;
a = a * r;
}
return product;
}
let a = 1, r = 2;
let N = 4;
document.write(productOfGP(a, r, N));
</script>
|
Time Complexity: O(N), where N is the given integer.
Auxiliary Space: O(1), as constant extra space is required.
Efficient Approach: The efficient approach is to observe that the product of all the N terms of the given geometric progression forms a formula:
The general G.P. is
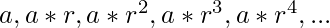
Product upto 1st term =
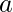
Product upto 2nd term =
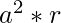
Product upto 3rd term =

Product upto 4th term =

.
.
.
Product upto N terms =
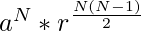
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float productOfGP(float a, float r,
int n)
{
return pow(a, n)
* pow(r, n * (n - 1) / 2);
}
int main()
{
float a = 1, r = 2;
int N = 4;
cout << productOfGP(a, r, N);
}
|
Java
class GFG{
static float productOfGP(float a, float r, int n)
{
return (float)Math.pow(a, n) *
(float)Math.pow(r, n * (n - 1) / 2);
}
public static void main(String s[])
{
float a = 1, r = 2;
int N = 4;
System.out.println(productOfGP(a, r, N));
}
}
|
Python3
def productOfGP(a, r, n):
return pow(a, n) * pow(r, n * (n - 1) // 2);
a = 1; r = 2;
N = 4;
print(productOfGP(a, r, N));
|
C#
using System;
class GFG{
static float productOfGP(float a, float r, int n)
{
return (float)Math.Pow(a, n) *
(float)Math.Pow(r, n * (n - 1) / 2);
}
public static void Main(String[] args)
{
float a = 1, r = 2;
int N = 4;
Console.WriteLine(productOfGP(a, r, N));
}
}
|
Javascript
<script>
function productOfGP(a, r, n)
{
return Math.pow(a, n) *
Math.pow(r, n * (n - 1) / 2);
}
let a = 1, r = 2;
let N = 4;
document.write(productOfGP(a, r, N));
</script>
|
Time Complexity: O(logN), for using pow function.
Auxiliary space: O(1), as constant extra space is required.
Another Approach:
Let there be a GP of N terms as followed:
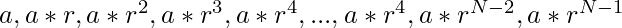
Product of 1st and last term =
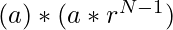
=
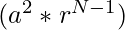
Product of 2nd and 2nd last term =
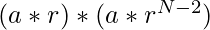
=
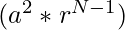
Product of 3rd and 3rd last term =
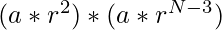
=
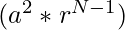
and so on…
In a geometric progression, the product of the first and the last term is the same as the product of the second and second last term and so on, no matter how many terms we are considering in a geometric progression.
Therefore, if
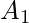 and
and 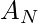 is the first and last terms of a GP, then the product of first N terms of the GP will be
is the first and last terms of a GP, then the product of first N terms of the GP will be
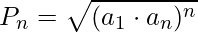
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float productOfGP(float a, float r,
int n)
{
int an = a * pow(r, n - 1);
return sqrt(pow(a * an, n));
}
int main()
{
float a = 1, r = 2;
int N = 4;
cout << productOfGP(a, r, N);
}
|
Java
import java.util.*;
class GFG{
static float productOfGP(float a, float r, int n)
{
int an = (int)(a * (int)(Math.pow(r, n - 1)));
return (int)Math.sqrt((int)Math.pow(a * an, n));
}
public static void main(String args[])
{
float a = 1, r = 2;
int N = 4;
System.out.print(productOfGP(a, r, N));
}
}
|
Python3
import math
def productOfGP(a, r, n):
an = a * pow(r, n - 1);
return (math.sqrt(pow(a * an, n)))
a = 1
r = 2;
N = 4;
print(productOfGP(a, r, N))
|
C#
using System;
class GFG{
static float productOfGP(float a, float r, int n)
{
int an = (int)(a * (int)(Math.Pow(r, n - 1)));
return (int)Math.Sqrt((int)Math.Pow(a * an, n));
}
public static void Main()
{
float a = 1, r = 2;
int N = 4;
Console.Write(productOfGP(a, r, N));
}
}
|
Javascript
<script>
function productOfGP(a, r, n)
{
let an = a * Math.pow(r, n - 1);
return Math.sqrt(Math.pow(a * an, n));
}
let a = 1, r = 2;
let N = 4;
document.write(productOfGP(a, r, N));
</script>
|
Time Complexity: O(logN), for using pow and sqrt functions.
Auxiliary space: O(1), as constant extra space is required.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...