Product of all Subsequences of size K except the minimum and maximum Elements
Last Updated :
09 Jun, 2022
Given an array A[] containing N elements and an integer K. The task is to calculate the product of all elements of subsequences of size K except the minimum and the maximum elements for each subsequence.
Note: Since the answer can be very large so print the final answer as mod of 109 + 7.
Examples:
Input : arr[] = {1, 2, 3 4}, K = 3
Output : 36
Subsequences of length 3 are:
{1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}
Excluding minimum and maximum elements from
each of the above subsequences, product will be:
(2 * 2 * 3 * 3) = 36.
Input : arr[] = {10, 5, 16, 6}, k=3
Output : 3600
Naive Approach: A simple approach is to generate all possible subsequences one by one and multiply all elements except maximum and minimum and further multiplying all of them. Since there will be a total of (n)C(K) subsequences all having K – 2 elements to be multiplied which is tedious work to do.
Efficient Approach: The idea is to first sort the array since it doesn’t matter if we consider subsequences or subsets.
Now count the occurrence of each element one by one.
In total, a number can occur in (n-1)C(K-1) subsequences out of which (i)C(K-1) times it will occur as maximum element and (n-i-1)C(K-1) times it will occur as a minimum element of that subsequence.
Hence, in total 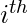 element will occur:
element will occur:
(n-1)C(K-1) - (i)C(K-1) - (n-i-1)C(K-1) times. (let's say it x)
So, at first we’ll be calculating x for each element a[i] and then multiply a[i] x times. i.e (![Rendered by QuickLaTeX.com a[i]^x mod(10^9 + 7)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8baa253819b7ac2e61ef1a77733df6bd_l3.png) ).
).
Since, It’s too difficult to calculate this for large arrays, so we’ll use Fermat’s Little Theorem.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MOD 1000000007
#define ll long long
#define max 101
ll C[max - 1][max - 1];
ll power(ll x, unsigned ll y)
{
unsigned ll res = 1;
x = x % MOD;
while (y > 0) {
if (y & 1) {
res = (res * x) % MOD;
}
y = y >> 1;
x = (x * x) % MOD;
}
return res % MOD;
}
void combi(int n, int k)
{
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = (C[i - 1][j - 1] % MOD
+ C[i - 1][j] % MOD) % MOD;
}
}
}
unsigned ll product(ll a[], int n, int k)
{
unsigned ll ans = 1;
sort(a, a + n);
ll powa = C[n - 1][k - 1];
for (int i = 0; i < n; i++) {
ll powla = C[i][k - 1];
ll powfa = C[n - i - 1][k - 1];
ll powe = ((powa % MOD) - (powla + powfa) % MOD + MOD) % MOD;
unsigned ll mul = power(a[i], powe) % MOD;
ans = ((ans % MOD) * (mul % MOD)) % MOD;
}
return ans % MOD;
}
int main()
{
combi(100, 100);
ll arr[] = { 1, 2, 3, 4 };
int n = sizeof(arr) / sizeof arr[0];
int k = 3;
unsigned ll ans = product(arr, n, k);
cout << ans << endl;
return 0;
}
|
Java
import java.util.Arrays;
class GFG
{
static int MOD= 1000000007;
static int max =101;
static long C[][] = new long[max ][max];
static long power(long x, long y)
{
long res = 1;
x = x % MOD;
while (y > 0)
{
if (y % 2== 1)
{
res = (res * x) % MOD;
}
y = y >> 1;
x = (x * x) % MOD;
}
return res % MOD;
}
static void combi(int n, int k)
{
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = (C[i - 1][j - 1] % MOD
+ C[i - 1][j] % MOD) % MOD;
}
}
}
static long product(long a[], int n, int k)
{
long ans = 1;
Arrays.sort(a);
long powa = C[n - 1][k - 1];
for (int i = 0; i < n; i++)
{
long powla = C[i][k - 1];
long powfa = C[n - i - 1][k - 1];
long powe = ((powa % MOD) - (powla + powfa) % MOD + MOD) % MOD;
long mul = power(a[i], powe) % MOD;
ans = ((ans % MOD) * (mul % MOD)) % MOD;
}
return ans % MOD;
}
public static void main(String[] args)
{
combi(100, 100);
long arr[] = { 1, 2, 3, 4 };
int n = arr.length;
int k = 3;
long ans = product(arr, n, k);
System.out.println(ans);
}
}
|
Python3
MOD = 1000000007
max = 101
C = [[0 for i in range(max)] for j in range(max)]
def power(x,y):
res = 1
x = x % MOD
while (y > 0):
if (y & 1):
res = (res * x) % MOD
y = y >> 1
x = (x * x) % MOD
return res % MOD
def combi(n, k):
for i in range(n + 1):
for j in range(min(i, k) + 1):
if (j == 0 or j == i):
C[i][j] = 1
else:
C[i][j] = (C[i - 1][j - 1] % MOD +
C[i - 1][j] % MOD) % MOD
def product(a, n, k):
ans = 1
a.sort(reverse = False)
powa = C[n - 1][k - 1]
for i in range(n):
powla = C[i][k - 1]
powfa = C[n - i - 1][k - 1]
powe = ((powa % MOD) - (powla + powfa) % MOD + MOD) % MOD
mul = power(a[i], powe) % MOD
ans = ((ans % MOD) * (mul % MOD)) % MOD
return ans % MOD
if __name__ == '__main__':
combi(100, 100)
arr = [1, 2, 3, 4]
n = len(arr)
k = 3
ans = product(arr, n, k)
print(ans)
|
C#
using System;
class GFG
{
static int MOD = 1000000007;
static int max = 101;
static long [,]C = new long[max, max];
static long power(long x, long y)
{
long res = 1;
x = x % MOD;
while (y > 0)
{
if (y % 2 == 1)
{
res = (res * x) % MOD;
}
y = y >> 1;
x = (x * x) % MOD;
}
return res % MOD;
}
static void combi(int n, int k)
{
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0;
j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
C[i, j] = 1;
else
C[i, j] = (C[i - 1, j - 1] % MOD +
C[i - 1, j] % MOD) % MOD;
}
}
}
static long product(long []a, int n, int k)
{
long ans = 1;
Array.Sort(a);
long powa = C[n - 1, k - 1];
for (int i = 0; i < n; i++)
{
long powla = C[i, k - 1];
long powfa = C[n - i - 1, k - 1];
long powe = ((powa % MOD) -
(powla + powfa) %
MOD + MOD) % MOD;
long mul = power(a[i], powe) % MOD;
ans = ((ans % MOD) *
(mul % MOD)) % MOD;
}
return ans % MOD;
}
static public void Main ()
{
combi(100, 100);
long []arr = { 1, 2, 3, 4 };
int n = arr.Length;
int k = 3;
long ans = product(arr, n, k);
Console.WriteLine(ans);
}
}
|
Javascript
<script>
let MOD= 1000000007;
let max =101;
let C = new Array(max);
for(let i = 0; i < max; i++)
{
C[i] = new Array(max);
for(let j = 0; j < max; j++)
{
C[i][j] = 0;
}
}
function power(x, y)
{
let res = 1;
x = x % MOD;
while (y > 0)
{
if (y % 2== 1)
{
res = (res * x) % MOD;
}
y = y >> 1;
x = (x * x) % MOD;
}
return res % MOD;
}
function combi(n, k)
{
let i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = (C[i - 1][j - 1] % MOD
+ C[i - 1][j] % MOD) % MOD;
}
}
}
function product(a, n, k)
{
let ans = 1;
a.sort(function(a, b){return a - b});
let powa = C[n - 1][k - 1];
for (let i = 0; i < n; i++)
{
let powla = C[i][k - 1];
let powfa = C[n - i - 1][k - 1];
let powe = ((powa % MOD) - (powla + powfa) % MOD + MOD) % MOD;
let mul = power(a[i], powe) % MOD;
ans = ((ans % MOD) * (mul % MOD)) % MOD;
}
return ans % MOD;
}
combi(100, 100);
let arr = [ 1, 2, 3, 4 ];
let n = arr.length;
let k = 3;
let ans = product(arr, n, k);
document.write(ans);
</script>
|
Time Complexity: O(nlogn + max*max), where n is the size of the given array and max is the defined constant.
Auxiliary Space: O(max*max), where max is the defined constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...