Probability that the pieces of a broken stick form a n sided polygon
Last Updated :
08 Jun, 2022
We have a stick of length L. The stick got broken at (n-1) randomly chosen points (lengths of parts can be non-integer or floating point numbers also) so we get n parts. We need to find the probability that these n pieces can form a n sided polygon.
Examples:
Input : L = 5 n = 3
Output : 0.25
We need to cut rope of length 5
into three parts.
First we need to find the condition when n lengths can form a n sided polygon. Let us consider a triangle, we know for a triangle the length of the largest side must be smaller than the sum of the lengths of other sides. Similarly for a n sided polygon the length of the largest side must be less than the sum of the other (n-1) sides. Why? Suppose we break the stick into two equal halves. We further break one of the halves into (n-1) parts. We can never place them such that they make a closed polygon. (Actually the best we can do is to make 2 parallel lines). So we just need to find the probability that no part has the length greater than or equal to L/2.
Now we need to work on the probability. There are many ways to calculate the required probability we will use a geometric approach. Consider a circle of perimeter L. We place n points on the perimeter. The probability that they lie on the same semicircle is 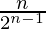 . Please refer this link for more information, let us denote it by P(E).
. Please refer this link for more information, let us denote it by P(E).
This probability is actually same as breaking the stick such that at least one part is of length L/2. But we want just the complement of this event hence our answer is 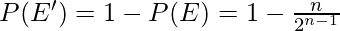
C++
#include<iostream>
using namespace std;
double printProbability(unsigned L, unsigned n)
{
unsigned p = (1 << (n-1));
return 1.0 - ((double)n) / ((double)p);
}
int main()
{
unsigned n = 3, L = 5;
cout << printProbability(L, n);
return 0;
}
|
Java
public class GFG {
static double printProbability(int L, int n)
{
int p = (1 << (n-1));
return 1.0 - ((double)n) / ((double)p);
}
public static void main(String args[])
{
int n = 3, L = 5;
System.out.println(printProbability(L, n));
}
}
|
Python3
def printProbability(L, n):
p = (1 << (n-1))
return 1.0 - (float(n) / float(p) )
if __name__=='__main__':
n = 3
L = 5
print(printProbability(L, n))
|
C#
using System;
class GFG
{
static double printProbability(int L, int n)
{
int p = (1 << (n - 1));
return 1.0 - ((double)n) /
((double)p);
}
public static void Main()
{
int n = 3, L = 5;
Console.WriteLine(printProbability(L, n));
}
}
|
PHP
<?php
function printProbability($L, $n)
{
$p = (1 << ($n - 1));
return 1.0 - ($n) / ($p);
}
$n = 3; $L = 5;
echo printProbability($L, $n);
?>
|
Javascript
<script>
function printProbability(L, n)
{
var p = (1 << (n - 1));
return 1.0 - n/ p;
}
var n = 3, L = 5;
document.write(printProbability(L, n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...