Probability is a branch of mathematics that deals with calculating the likelihood of a given event’s occurrence. It is expressed as a number between 0 and 1.
Let’s learn about the basic probability concepts, their formulas, types and examples.

Probability Definition
Probability is the measure of the likelihood that an event will occur. It is quantified as a number between 0 and 1.
The values of probability range from 0 to 1, with 0 telling us improbability and 1 denoting certainty.
For calculating probability, we simply divide the number of favorable outcomes by the total number of outcomes.
Probability Theory
Probability theory is a branch of mathematics that deals with the interpretation of random events and the likelihood of these events occurring.
Probability theory starts with basic concepts such as random experiments, sample spaces, events, and the probability of events.
A random experiment is any process or action that results in one of several possible outcomes, like tossing a coin or rolling a die. The sample space is the set of all possible outcomes of an experiment, and an event is a specific outcome or a set of outcomes.
Terms in Probability
Here are some basic concepts or terminologies used in probability:
| Term |
Definition |
| Sample Space |
The set of all possible outcomes in a probability experiment. For instance, in a coin toss, it’s “head” and “tail”. |
| Sample Point |
One of the possible results in an experiment. For example, in rolling a fair six-sided dice, sample points are 1 to 6. |
| Experiment |
A process or trial with uncertain results. Examples include coin tossing, card selection, or rolling a die. |
| Event |
A subset of the sample space representing certain outcomes. Example: getting “1” when rolling a die. |
| Favorable Outcome |
An outcome that produces the desired or expected consequence. |
Probability of an Event
The probability of an event is a measure of the likelihood that the event will occur, expressed as a number between 0 and 1.
An event with a probability of 1 is considered certain to happen, while an event with a probability of 0 is certain not to happen.
Let’s discuss different types of events in probability.
Equally Likely Events
Equally likely events are those whose chances or probabilities of happening are equal. Both events are not related to one another.
For example, there are equal possibilities of receiving either a head or a tail when we flip a coin.
Exhaustive Events
We call an event exhaustive when the set of all experiment results is the same as the sample space.
Mutually Exclusive Events
Events that are mutually exclusive cannot occur at the same time.
For instance, the weather may be hot or chilly simultaneously. We can’t have the same weather at the same time.

Sample Space Illustration in Probability
Complimentary events
The non-occurring events. The complement of an event A is the event, not A(or A’).
Also Read: Mathematics | Probability
P(E) = Number of favorable outcomes / Total number of outcomes
Note: where P(E) denotes the probability of an event E.
This formula defines the possibility of an event occurring. It is defined as the ratio of the number of favorable outcomes to the total number of outcomes.
Probability Tree Diagram
A tree diagram in probability is a graphic representation that helps us in determining the likely outcomes that is whether an event will occur or not. It helps us understand the all possibilities of an event and which possibilities can occur and cannot occur.
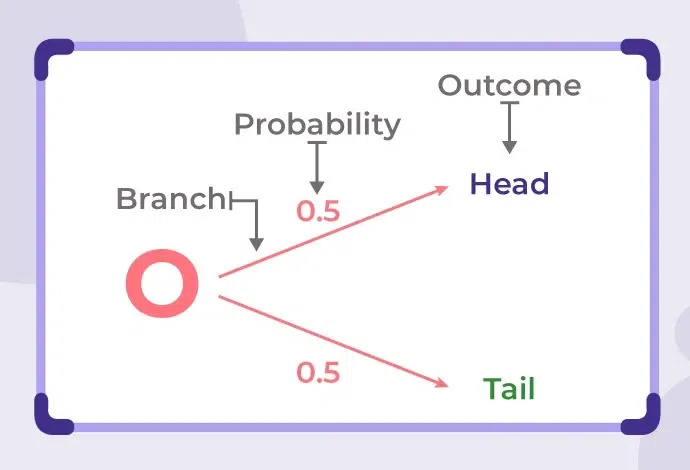
Types of Probability
These are 3 major types of probability:
- Theoretical Probability
- Experimental Probability
- Axiomatic Probability
Theoretical Probability
It is focused on the likelihood of anything occurring. The reasoning behind probability is the foundation of scientific probability.
If a coin is flipped, the statistical chance of having a head is 1/2. An event’s statistical chance is the chance that the occurrence will occur. It is determined by dividing the number of desirable outcomes by the total number of outcomes is thus termed theoretical probability.
Learn More :
- Chance and Probability
- Empirical Probability
- Probability Theory
- Addition Rule for Probability
- Practice Problems on Probability
Experimental Probability
It is founded on the results of an experiment. The experimental chance can be determined by dividing the total number of trials by the number of potential outcomes.
For example, if a coin is flipped ten times and heads are reported six times, the experimental chance of heads is 6/10 or 3/5.
Learn More :
- Experimental Probability
- Dependent and Independent Events
- Random Experiments
- Event
- Types of Events in Probability
- Variance and Standard Deviation
- Frequency Distributions
- Measure of Dispersion
Axiomatic Probability
A collection of laws or axioms that apply to all forms is established in axiomatic probability. Kolmogorov developed these axioms, which are known as Kolmogorov’s three axioms.
The axiomatic approach to probability quantifies the likelihood of events occurring or not occurring.
Learn More :
- Axiomatic Approach to Probability
- Conditional Probability and Independence
- Multiplication Theorem
- Dependent and Independent Event
- Bayes’ Theorem
- Probability Distribution
- Binomial Random Variables and Binomial Distribution
- Binomial Mean and Standard Deviation
- Bernoulli Trials and Binomial Distribution
- Discrete Random Variables
- Expected Value
Probability Theorems
Some of the most important theorems of probability are :
| Theorem |
Description |
| Theorem 1 |
The sum of the probability of an event and its complement is 1, i.e., P(A) +P(A′) = 1 |
| Theorem 2 |
The probability of an impossible event or an event not happening is always 0, i.e, P(∅) = 0 |
| Theorem 3 |
The probability of a sure event is always 1, i.e, P(A )= 1. |
| Theorem 4 |
The probability of any event lies between 0 and 1, i.e, 0 < P(A) <1. |
| Theorem 5 |
Formula for the union of two events A and B: P(A∪B) = P(A) + P(B) − P(A∩B) |
|
For mutually exclusive events A and B: P(A∪B) = P(A) + P(B) |
| Additional Formulas |
1. Probability of union of two events: P(A∪B) = P(A) +P(B) −P(A∩B) |
| 2. Probability of the complement of an event: P(A′)=1 − P(A) |
| 3. Conditional probability: P(A∣B) = P(B)P(A∩B) |
| 4. Probability of intersection of two events: P(A∩B)=P(A)×P(B∣A) |
Bayes’ Theorem on Conditional Probability
Bayes’ Theorem defines the probability of an event based on the condition of occurrence of other events. It is also called conditional probability.
It helps in calculating the probability of occurrence of one event based on the condition that another event is also taking place or occurring.
For example, let us assume you have two bags of marbles in various colors. Bag A has three red and two blue marbles, while bag B has one red and four blue marbles. You pick one of the bags at random, then you pick a marble at random from that bag. Given that you selected a red marble, what is the probability that you selected bag A? Such probability is called conditional probability.
Learn More:
Following is the Bayes’ Theorem Formula :
P(A|B) = P(B|A)⋅P(A) P(B)
where:
- P(A|B) denotes how often event A happens on a condition that B happens.
- P(B|A) denotes how often event B happens on a condition that A happens.
- P(A) is the probability of event A occurring.
- P(B) is the probability of event B occur.
Probability Density Function
Probability density function is defined as a function that contains all the possible outcomes of any given situation.
It used to specify the probability of a continuous random variable falling within a particular range of values. Unlike discrete random variables which have probabilities associated with specific points, continuous random variables require a function to define their probabilities over an interval. It is also known as the Probability Distribution Function.
Common Probability Problems
We will now see some common probability problems that are given in school tests. This will prepare you for the questions and you can understand the methodology to solve them.
1. Probability of Tossing Coin
Now let us take into account the case of coin tossing to understand probability in a better way.
A) Tossing a Coin
A single coin when flipped has two possible outcomes, a head or a tail. The definition of probability when applied here to find the probability of getting a head or getting a tail.
The total number of possible outcomes = 2
Sample Space = {H, T} H: Head, T: Tail
- P(H) = Number of Heads/ Total Number of outcomes = 1/2
- P(T) = Number of Tails/ Total Number of outcomes = 1/2
B) Tossing Two Coins
There are a total of four possible results when tossing two coins. We can calculate the probability of two heads or two tails using the formula.
The probability of getting two tails can be calculated as :
Total number of outcomes = 4
Sample Space = {(H,H),(H,T),(T,H),(T,T)}
- P(2T) = P(0H) = Number of outcomes with two tails/ Total number of outcomes = 1/4
- P(1H) = P(1T) = Number of outcomes with one head/ Total number of outcomes = 2/4 = 1/2
C ) Probability of Tossing Three Coins
The number of total outcomes on tossing three coins is 23 = 8. For these outcomes, we can find the probability of various cases such as getting one tail, two tails, three tails, and no tails, and similarly can be calculated for several heads.
Total number of outcomes = 23 = 8
Sample space = {(H, H, H), (H, H, T),(H, T, H), (T, H, H), (T, T, H), (T, H, T), (H, T, T), (T, T, T)}.
P(3T) = P(0 H) = Number of outcomes with three tails/ Total Number of outcomes = 1/8
2. Probability of Rolling Dice
Various games use dice to decide the movements of the player during the games. A dice has six outcomes. Some games are played using two dice. Now let us calculate the outcomes, and their probabilities for one dice and two dice respectively.
Rolling One Dice
The number of outcomes is 6 when a die is rolled and the sample space is = {1,2,3,4,5,6}.
Let us now discuss some cases.
- P(Even Number) = Number of outcomes in which even number occur/Total Outcomes = 3/6 = 1/2
- P(Prime Number) = Number of prime number outcomes/ Total Outcomes = 3/6 = 1/2
Rolling Two Dice
The number of total outcomes, when two dice are rolled, is 62 = 36.

Probability of Rolling Two Dice
Let us check a few cases in the above example,
- Probability of getting a doublet(Same number) = 6/36 = 1/6
- Probability of getting a number 3 on at least one dice = 11/36
3. Probability of Cards
Spades, clubs, diamonds, and hearts make up the four suits that form a deck of 52 playing cards. There are a total of 52 cards, with 13 in each of the four suits (clubs, diamonds, hearts, and spades). The symbols for the cards are listed below.
.png)
Black cards are spades and clubs. Red cards are hearts and diamonds. Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, queen, and King are the 13 cards that make up each suit. The jack, queen, and king are referred to as face cards in these.
- Probability of getting a black card is P(Black Card) = 26/52 = 1/2
- Probability of getting a heart is P(Heart) = 13/52 = 1/4
- Probability of getting a face card is P(Face card) = 12/52 = 3/13
Related Articles:
Probability Examples and Solutions
We have provided you with some probability problems with their solutions.
Problem 1. There are 8 balls in a container, 4 are red, 1 is yellow and 3 are blue. What is the probability of picking a yellow ball?

Probability of picking a ball
Solution:
The probability is equal to the number of yellow balls in the container divided by the total number of balls in the container, i.e. 1/8.
Problem 2: A dice is rolled. What is the probability that an even number has been obtained?

Probability of Rolling a Dice
Solution:
When fair six-sided dice are rolled, there are six possible outcomes: 1, 2, 3, 4, 5, or 6.
Out of these, half are even (2, 4, 6) and half are odd (1, 3, 5). Therefore, the probability of getting an even number is:
P(even) = number of even outcomes / total number of outcomes
P(even) = 3 / 6
P(even) = 1/2
Problem 3. A bag contains 4 white, 5 red, and 6 blue balls. Three balls are drawn at random from the bag. The probability that all of them are red, is:
Solution:
Let S be the sample space.
Then, n(S) = Number of ways of drawing 3 balls out of 15
= 15C3 = 455
Let E = event of getting all the 3 red balls.
n(E) = 5C3 = 10
P(E) = n(E)/n(S) = 10/455 = 2/91.
Problem 4. In a class there are 10 girls and 15 boys, what is the probability that 1 girl and 2 boys are selected?
Solution:
Let S be the sample space.
Then, n(S)= Number of ways of selecting 3 children out of 25
= 25C3
= 2300.
Let E= event of selecting 1 girl and 2 boys.
n(E) = 10C1*15C2 = 1050
P(E) = n(E)/n(S) = 1050/2300 = 21/46.
Conclusion of Probability in Maths
Probability in Maths is the likelihood that an event will occur. It’s similar to picking whether your favorite team will win a game or whether it will rain tomorrow. Probability is the study of the likelihood of an event or the possible outcomes under specific circumstances. For instance, we might be interested in finding out how often it is to draw a red ball from a bag of colored balls or what the odds are of flipping a coin and receiving heads. We may make sense of uncertainty and well-informed decisions by using probability to compare the chances of various scenarios. It’s a helpful tool in many fields, such as evaluating risks in banking, forecasting game outcomes, and even interpreting data in science.
Probability in Maths on FAQs
What is Probability in Maths?
Probability is a branch of mathematics that is a measure of how probable an incident is to occur. For example, when a coin is tossed in the air, there are two possible outcomes head or tail.
How many Types of Probability are there?
There are three types of probability :
- Theoretical Probability
- Experimental Probability
- Axiomatic Probability
What is the Probability Formula?
P(E) = Number of favorable outcomes /Total number of outcomes
where, P(E) denotes the probability of an event E.
What is Conditional Probability?
Conditional probability is a measure of the probability of an event occurring, given that another event has already occurred. This concept is fundamental in probability theory and statistics, and it’s denoted as P(A|B), which is read as “the probability of A given B.”
How do I Calculate Probability?
To Calculate the probability of an event, find the ratio of the number of favorable outcomes to the total outcomes in that sample space. It is expressed as, Probability of an event P(E) = (Number of favorable outcomes) ÷ (Number of Elements in Sample space).
What is Probability of Impossible Event?
The probability of an impossible event is zero.
What is Probability Density Function?
A Probability Density Function (PDF) represents the likelihood of a continuous random variable falling within a particular range of values. It is a statistical concept used in probability theory and statistics.
What is Probability Mass Function ?
A Probability Mass Function (PMF) represents the probability distribution of a discrete random variable, which can take on a finite or countably infinite number of possible values.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...