Printing all solutions in N-Queen Problem
Last Updated :
09 Oct, 2023
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, the following is a solution for 4 Queen problem.
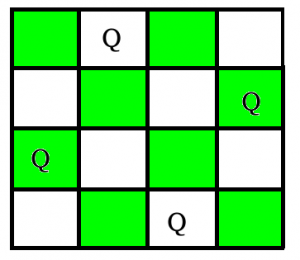
In previous post, we have discussed an approach that prints only one possible solution, so now in this post, the task is to print all solutions in N-Queen Problem. Each solution contains distinct board configurations of the N-queens’ placement, where the solutions are a permutation of [1,2,3..n] in increasing order, here the number in the ith place denotes that the ith-column queen is placed in the row with that number. For the example above solution is written as [[2 4 1 3 ] [3 1 4 2 ]]. The solution discussed here is an extension of the same approach.
Backtracking Algorithm
The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column. Do following
for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing queen in [row, column] leads to a
solution then return true.
c) If placing queen doesn't lead to a solution
then unmark this [row, column] (Backtrack)
and go to step (a) to try other rows.
4) If all rows have been tried and nothing worked,
return false to trigger backtracking.
A modification is that we can find whether we have a previously placed queen in a column or in left diagonal or in right diagonal in O(1) time. We can observe that
- For all cells in a particular left diagonal , their row + col = constant.
- For all cells in a particular right diagonal, their row – col + n – 1 = constant.
Let say n = 5, then we have a total of 2n-1 left and right diagonals
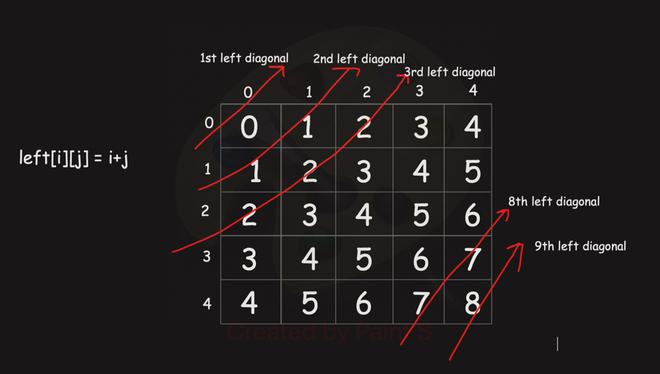
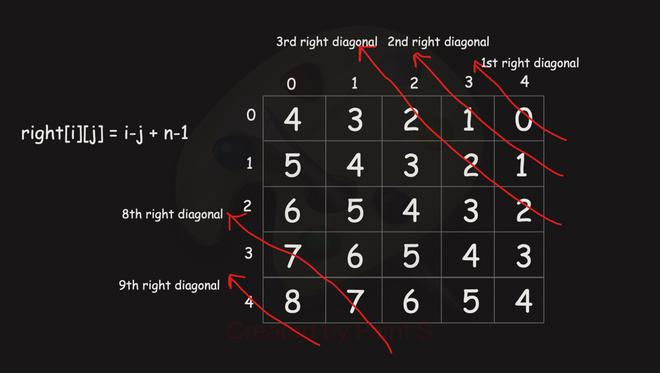
Let say we placed a queen at (2,0)
(2,0) have leftDiagonal value = 2. Now we can not place another queen at (1,1) and (0,2) because both of these have same leftDiagonal value as for (2,0). Similar thing can be noticed for right diagonal as well.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > result;
bool isSafe(vector<vector<int> > board,
int row, int col)
{
int i, j;
int N = board.size();
for (i = 0; i < col; i++)
if (board[row][i])
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j])
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j])
return false;
return true;
}
bool solveNQUtil(vector<vector<int> >& board, int col)
{
int N = board.size();
if (col == N) {
vector<int> v;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (board[i][j] == 1)
v.push_back(j + 1);
}
}
result.push_back(v);
return true;
}
bool res = false;
for (int i = 0; i < N; i++) {
if (isSafe(board, i, col)) {
board[i][col] = 1;
res = solveNQUtil(board, col + 1) || res;
board[i][col] = 0;
}
}
return res;
}
vector<vector<int> > nQueen(int n)
{
result.clear();
vector<vector<int> > board(n, vector<int>(n, 0));
if (solveNQUtil(board, 0) == false) {
return {};
}
sort(result.begin(), result.end());
return result;
}
int main()
{
int n = 4;
vector<vector<int> > v = nQueen(n);
for (auto ar : v) {
cout << "[";
for (auto it : ar)
cout << it << " ";
cout << "]";
}
return 0;
}
|
Java
import java.util.*;
class GfG {
static List<List<Integer>> nQueen(int n) {
cols = new boolean[n];
leftDiagonal = new boolean[2*n];
rightDiagonal = new boolean[2*n];
result = new ArrayList<>();
List<Integer> temp = new ArrayList<>();
for(int i=0;i<n;i++)temp.add(0);
solveNQUtil(result,n,0,temp);
return result;
}
private static void solveNQUtil(List<List<Integer>> result,int n,int row,List<Integer> comb){
if(row==n){
result.add(new ArrayList<>(comb));
return;
}
for(int col = 0;col<n;col++){
if(cols[col] || leftDiagonal[row+col] || rightDiagonal[row-col+n])
continue;
cols[col] = leftDiagonal[row+col] = rightDiagonal[row-col+n] = true;
comb.set(col,row+1);
solveNQUtil(result,n,row+1,comb);
cols[col] = leftDiagonal[row+col] = rightDiagonal[row-col+n] = false;
}
}
static List<List<Integer> > result
= new ArrayList<List<Integer> >();
static boolean[] cols,leftDiagonal,rightDiagonal;
public static void main(String[] args)
{
int n = 4;
List<List<Integer> > res = nQueen(n);
System.out.println(res);
}
}
|
Python3
result = []
def isSafe(board, row, col):
for i in range(col):
if (board[row][i]):
return False
i = row
j = col
while i >= 0 and j >= 0:
if(board[i][j]):
return False
i -= 1
j -= 1
i = row
j = col
while j >= 0 and i < 4:
if(board[i][j]):
return False
i = i + 1
j = j - 1
return True
def solveNQUtil(board, col):
if (col == 4):
v = []
for i in board:
for j in range(len(i)):
if i[j] == 1:
v.append(j+1)
result.append(v)
return True
res = False
for i in range(4):
if (isSafe(board, i, col)):
board[i][col] = 1
res = solveNQUtil(board, col + 1) or res
board[i][col] = 0
return res
def solveNQ(n):
result.clear()
board = [[0 for j in range(n)]
for i in range(n)]
solveNQUtil(board, 0)
result.sort()
return result
n = 4
res = solveNQ(n)
print(res)
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GfG {
static List<List<int> > result = new List<List<int> >();
static bool isSafe(int[, ] board, int row, int col,
int N)
{
int i, j;
for (i = 0; i < col; i++)
if (board[row, i] == 1)
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i, j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i, j] == 1)
return false;
return true;
}
static bool solveNQUtil(int[, ] board, int col, int N)
{
if (col == N) {
List<int> v = new List<int>();
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++) {
if (board[i, j] == 1)
v.Add(j + 1);
}
result.Add(v);
return true;
}
bool res = false;
for (int i = 0; i < N; i++) {
if (isSafe(board, i, col, N)) {
board[i, col] = 1;
res = solveNQUtil(board, col + 1, N) || res;
board[i, col] = 0;
}
}
return res;
}
static List<List<int> > solveNQ(int n)
{
result.Clear();
int[, ] board = new int[n, n];
solveNQUtil(board, 0, n);
return result;
}
public static void Main()
{
int n = 4;
List<List<int> > res = solveNQ(n);
for (int i = 0; i < res.Count; i++) {
Console.Write("[");
for (int j = 0; j < res[i].Count; j++) {
Console.Write(res[i][j]+ " ");
}
Console.Write("]");
}
}
}
|
Javascript
let result = []
function isSafe(board, row, col)
{
for (let i = 0; i < col; i++)
if (board[row][i])
return false
let i = row
let j = col
while (i >= 0 && j >= 0)
{
if(board[i][j])
return false
i -= 1
j -= 1
}
i = row
j = col
while (j >= 0 && i < 4)
{
if(board[i][j])
return false
i = i + 1
j = j - 1
}
return true
}
function solveNQUtil(board, col)
{
if (col == 4)
{
let v = []
for (let i of board)
{
for (var j = 0; j < i.length; j++)
{
if (i[j] == 1)
v.push(j+1)
}
}
result.push(v)
return true
}
let res = false
for (var i = 0; i < 4; i++)
{
if (isSafe(board, i, col))
{
board[i][col] = 1
res = solveNQUtil(board, col + 1) || res
board[i][col] = 0
}
}
return res
}
function solveNQ(n)
{
result = []
let board = new Array(n);
for (var i = 0; i < n; i++)
board[i] = new Array(n).fill(0)
solveNQUtil(board, 0)
result.sort()
return result
}
let n = 4
let res = solveNQ(n)
console.log(res)
|
Output
[2 4 1 3 ][3 1 4 2 ]
Time Complexity: O(N!), where N is the size of the chessboard.
Auxiliary Space: O(N^2)
Efficient Backtracking Approach Using Bit-Masking
Algorithm:
There is always only one queen in each row and each column, so idea of backtracking is to start placing queen from the leftmost column of each row and find a column where the queen could be placed without collision with previously placed queens. It is repeated from the first row till the last row. While placing a queen, it is tracked as if it is not making a collision (row-wise, column-wise and diagonally) with queens placed in previous rows. Once it is found that the queen can’t be placed at a particular column index in a row, the algorithm backtracks and change the position of the queen placed in the previous row then moves forward to place the queen in the next row.
- Start with three-bit vector which is used to track safe place for queen placement row-wise, column-wise and diagonally in each iteration.
- Three-bit vector will contain information as bellow:
- rowmask: set bit index (i) of this bit vector will indicate, the queen can’t be placed at ith column of next row.
- ldmask: set bit index (i) of this bit vector will indicate, the queen can’t e placed at ith column of next row. It represents the unsafe column index for next row falls under left diagonal of queens placed in previous rows.
- rdmask: set bit index (i) of this bit vector will indicate, the queen can’t be placed at ith column of next row. It represents the unsafe column index for next row falls right diagonal of queens placed in previous rows.
- There is a 2-D (NxN) matrix (board), which will have ‘ ‘ character at all indexes in beginning and it gets filled by ‘Q’ row-by-row. Once all rows are filled by ‘Q’, the current solution is pushed into the result list.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > result;
void solveBoard(vector<vector<char> >& board, int row,
int rowmask, int ldmask, int rdmask,
int& ways)
{
int n = board.size();
int all_rows_filled = (1 << n) - 1;
if (rowmask == all_rows_filled) {
vector<int> v;
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board.size(); j++) {
if (board[i][j] == 'Q')
v.push_back(j + 1);
}
}
result.push_back(v);
return;
}
int safe
= all_rows_filled & (~(rowmask | ldmask | rdmask));
while (safe) {
int p = safe & (-safe);
int col = (int)log2(p);
board[row][col] = 'Q';
solveBoard(board, row + 1, rowmask | p,
(ldmask | p) << 1, (rdmask | p) >> 1,
ways);
safe = safe & (safe - 1);
board[row][col] = ' ';
}
return;
}
int main()
{
int n = 4;
int ways = 0;
vector<vector<char> > board;
for (int i = 0; i < n; i++) {
vector<char> tmp;
for (int j = 0; j < n; j++) {
tmp.push_back(' ');
}
board.push_back(tmp);
}
int rowmask = 0, ldmask = 0, rdmask = 0;
int row = 0;
result.clear();
solveBoard(board, row, rowmask, ldmask, rdmask, ways);
sort(result.begin(),result.end());
for (auto ar : result) {
cout << "[";
for (auto it : ar)
cout << it << " ";
cout << "]";
}
return 0;
}
|
Java
import java.util.*;
public class NQueenSolution {
static List<List<Integer> > result
= new ArrayList<List<Integer> >();
public void solveBoard(char[][] board, int row,
int rowmask, int ldmask,
int rdmask)
{
int n = board.length;
int all_rows_filled = (1 << n) - 1;
if (rowmask == all_rows_filled) {
List<Integer> v = new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'Q')
v.add(j + 1);
}
}
result.add(v);
return;
}
int safe = all_rows_filled
& (~(rowmask | ldmask | rdmask));
while (safe > 0) {
int p = safe & (-safe);
int col = (int)(Math.log(p) / Math.log(2));
board[row][col] = 'Q';
solveBoard(board, row + 1, rowmask | p,
(ldmask | p) << 1,
(rdmask | p) >> 1);
safe = safe & (safe - 1);
board[row][col] = ' ';
}
}
public void printBoard(char[][] board)
{
for (int i = 0; i < board.length; i++) {
System.out.print("|");
for (int j = 0; j < board[i].length; j++) {
System.out.print(board[i][j] + "|");
}
System.out.println();
}
}
public static void main(String args[])
{
int n = 4;
char board[][] = new char[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[i][j] = ' ';
}
}
int rowmask = 0, ldmask = 0, rdmask = 0;
int row = 0;
NQueenSolution solution = new NQueenSolution();
result.clear();
solution.solveBoard(board, row, rowmask, ldmask,
rdmask);
System.out.println(result);
}
}
|
Python3
import math
result = []
def solveBoard(board, row, rowmask,
ldmask, rdmask):
n = len(board)
all_rows_filled = (1 << n) - 1
if (rowmask == all_rows_filled):
v = []
for i in board:
for j in range(len(i)):
if i[j] == 'Q':
v.append(j+1)
result.append(v)
safe = all_rows_filled & (~(rowmask |
ldmask | rdmask))
while (safe > 0):
p = safe & (-safe)
col = (int)(math.log(p)/math.log(2))
board[row][col] = 'Q'
solveBoard(board, row+1, rowmask | p,
(ldmask | p) << 1, (rdmask | p) >> 1)
safe = safe & (safe-1)
board[row][col] = ' '
def printBoard(board):
for row in board:
print("|" + "|".join(row) + "|")
def main():
n = 4
board = []
for i in range(n):
row = []
for j in range(n):
row.append(' ')
board.append(row)
rowmask = 0
ldmask = 0
rdmask = 0
row = 0
result.clear()
solveBoard(board, row, rowmask, ldmask, rdmask)
result.sort()
print(result)
if __name__ == "__main__":
main()
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
public class NQueenSolution{
static List<List<int>> result = new List<List<int>>();
public void solveBoard(char[,] board, int row,int rowmask, int ldmask,int rdmask)
{
int n = board.GetLength(0);
int all_rows_filled = (1 << n) - 1;
if (rowmask == all_rows_filled) {
List<int> v = new List<int>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (board[i,j] == 'Q')
v.Add(j + 1);
}
}
result.Add(v);
return;
}
int safe = ((all_rows_filled) & (~(rowmask | ldmask | rdmask)));
while (safe > 0) {
int p = safe & (-safe);
int col = (int)(Math.Log(p) / Math.Log(2));
board[row,col] = 'Q';
solveBoard(board, row + 1, rowmask | p,
(ldmask | p) << 1,
(rdmask | p) >> 1);
safe = safe & (safe - 1);
board[row,col] = ' ';
}
}
public void printBoard(char[,] board)
{
for (int i = 0; i < board.GetLength(0); i++) {
Console.Write("|");
for (int j = 0; j < board.GetLength(1); j++) {
Console.Write(board[i,j] + "|");
}
Console.Write("\n");
}
}
static public void Main (){
int n = 4;
char[,] board = new char[n,n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[i,j] = ' ';
}
}
int rowmask = 0, ldmask = 0, rdmask = 0;
int row = 0;
NQueenSolution solution = new NQueenSolution();
result.Clear();
solution.solveBoard(board, row, rowmask, ldmask,rdmask);
foreach (var sublist in result)
{
Console.Write("[");
foreach (int item in sublist)
{
Console.Write(item+" ");
}
Console.Write("]");
}
}
}
|
Javascript
let result = []
function solveBoard(board, row, rowmask,
ldmask, rdmask)
{
let n = (board).length
let all_rows_filled = (1 << n) - 1
if (rowmask == all_rows_filled)
{
let v = []
for (let i of board)
for (var j = 0; j < i.length; j++)
{
if (i[j] == 'Q')
v.push(j+1)
}
result.push(v)
}
let safe = all_rows_filled & (~(rowmask |
ldmask | rdmask))
while (safe > 0)
{
let p = safe & (-safe)
let col = Math.floor(Math.log(p)/Math.log(2))
board[row][col] = 'Q'
solveBoard(board, row+1, rowmask | p,
(ldmask | p) << 1, (rdmask | p) >> 1)
safe = safe & (safe-1)
board[row][col] = ' '
}
}
// Program to print board
function printBoard(board)
{
for (let row of board)
print("|" + (row).join( "|") + "|")
}
// Driver Code
let n = 4 // board size
let board = []
for (var i = 0; i < n; i++)
{
let row = []
for (var j = 0; j < n; j++)
row.push(' ')
board.push(row)
}
let rowmask = 0
let ldmask = 0
let rdmask = 0
let row = 0
result = []
solveBoard(board, row, rowmask, ldmask, rdmask)
result.sort()
console.log(result)
|
Output
[2 4 1 3 ][3 1 4 2 ]
Iterative backtracking solution:
In this section of the article, an iterative backtracking solution without recursion is introduced. The code will mainly utilize two nested loops and a stack to keep track of the positions of queens on the board and use this stack to backtrack.
Algorithm:
n: is the number of rows, columns, and queens to be added.
1- Create 2D-array to represent the board with each cell in the array corresponding to a box in the board
2- Create a stack to keep track of the queens' positions where the queen on the top is always the most recently added queen.
3- set counter j = 1 which will be used loop through columns in the coming steps.
4- Create an outer loop through the rows from i = 1 ----> i = n
5- Create inner loop through columns from j ----> j = n.
6- in the inner body of loops check if the current cell is valid to add a queen
if valid
- add the queen to the board
- add the queen's position to the stack
- break the inner loop
7- after finishing or breaking the inner loop
a) set j = 1 (so the default is to start looping through the columns from j = 1 in the coming iteration)
b) check if the size of the stack equals the number of the row to see if a queen was placed in current row
if no queen was placed:
8- back track to the last added queen by doing the following:
a) accessing the position of the last added queen from the top of stack
b) delete the last added queen from the board
c) set i (counter for rows of the board) = the row of the last added queen
d) set j = the column of last added queen + 1
9- if i == n meaning that all rows are now visited and filled with queens
a) print solution
b) do step 8 again to test other solutions until the stack is empty
According to the below Implementation, the solutions will be printed as an n*n matrix of zeros and ones, where the cells = 1 represent the queens.
Below is the Implementation of the above algorithm
C++
#include <iostream>
#include <stack>
#include <utility>
#include <vector>
using namespace std;
using vvi = vector<vector<int> >;
using vi = vector<int>;
void print(vvi board)
{
int count = 0;
for (auto& row : board) {
for (auto& el : row)
if (el == 1)
count++;
}
if (count != board.size())
return;
for (auto& row : board) {
for (auto& el : row)
cout << el << " ";
cout << '\n';
}
}
bool validate(vvi board, int i, int j)
{
for (int c = 1; c <= j; c++)
if (board[i - 1] == 1)
return false;
for (int r = 1; r <= i; r++)
if (board[r - 1][j - 1] == 1)
return false;
int c = j;
int r = i;
while (c != 0 and r != 0) {
if (board[r - 1] == 1)
return false;
r--;
c--;
}
c = j;
r = i;
while (c != board.size() + 1 and r != 0) {
if (board[r - 1] == 1)
return false;
r--;
c++;
}
return true;
}
void n_queen(int n)
{
vvi board(n, vi(n));
stack<pair<int, int> >
queens_positions;
int j = 1;
for (int i = 1; i <= board.size(); i++) {
for (; j <= board.size(); j++) {
if (validate(board, i,
j)) {
board[i - 1][j - 1] = 1;
queens_positions.push(make_pair(i, j));
break;
}
}
j = 1;
if (queens_positions.size()
!= i) {
if (!queens_positions.empty()) {
pair<int, int> Q_last
= queens_positions
.top();
queens_positions.pop();
board[Q_last.first - 1][Q_last.second - 1]
= 0;
i = Q_last.first
- 1;
j = Q_last.second
+ 1;
}
}
if (i == board.size()) {
print(board);
cout << '\n';
if (!queens_positions.empty()) {
pair<int, int> Q_last
= queens_positions
.top();
queens_positions.pop();
board[Q_last.first - 1][Q_last.second - 1]
= 0;
i = Q_last.first
- 1;
j = Q_last.second
+ 1;
}
}
}
}
int main() { n_queen(4); }
|
Java
import java.util.*;
public class NQueenProblem {
static void print(int[][] board)
{
int count = 0;
for (int[] row : board) {
for (int el : row) {
if (el == 1) {
count++;
}
}
}
if (count != board.length) {
return;
}
for (int[] row : board) {
for (int el : row) {
System.out.print(el + " ");
}
System.out.println();
}
}
static boolean validate(int[][] board, int i, int j)
{
for (int c = 1; c <= j; c++) {
if (board[i - 1] == 1) {
return false;
}
}
for (int r = 1; r <= i; r++) {
if (board[r - 1][j - 1] == 1) {
return false;
}
}
int c = j;
int r = i;
while (c != 0 && r != 0) {
if (board[r - 1] == 1) {
return false;
}
r--;
c--;
}
c = j;
r = i;
while (c != board.length + 1 && r != 0) {
if (board[r - 1] == 1) {
return false;
}
r--;
c++;
}
return true;
}
static void nQueen(int n)
{
int[][] board = new int[n][n];
Stack<int[]> queensPositions
= new Stack<>();
int j = 1;
for (int i = 1; i <= board.length; i++) {
for (; j <= board.length; j++) {
if (validate(board, i, j)) {
board[i - 1][j - 1] = 1;
queensPositions.push(
new int[] { i, j });
break;
}
}
j = 1;
if (queensPositions.size() != i) {
if (!queensPositions.empty()) {
int[] qLast = queensPositions.pop();
board[qLast[0] - 1][qLast[1] - 1]
= 0;
i = qLast[0]
- 1;
j = qLast[1]
+ 1;
}
}
if (i == board.length) {
print(board);
System.out.println();
if (!queensPositions.empty()) {
int[] qLast = queensPositions.pop();
board[qLast[0] - 1][qLast[1] - 1]
= 0;
i = qLast[0]
- 1;
j = qLast[1]
+ 1;
}
}
}
}
public static void main(String[] args) { nQueen(4); }
}
|
Python3
class NQueenProblem:
def print_board(board):
count = 0
for row in board:
for el in row:
if el == 1:
count += 1
if count != len(board):
return
for row in board:
for el in row:
print(el, end=" ")
print()
def validate(board, i, j):
for c in range(j):
if board[i] == 1:
return False
for r in range(i):
if board[r][j] == 1:
return False
r, c = i, j
while c >= 0 and r >= 0:
if board[r] == 1:
return False
r -= 1
c -= 1
r, c = i, j
while c < len(board) and r >= 0:
if board[r] == 1:
return False
r -= 1
c += 1
return True
def n_queen(n):
solutions = []
board = [[0] * n for _ in range(n)]
stack = []
row, col = 0, 0
while True:
while col < n:
if NQueenProblem.validate(board, row, col):
board[row][col] = 1
stack.append((row, col))
col = 0
break
col += 1
else:
if not stack:
break
row, col = stack.pop()
board[row][col] = 0
col += 1
continue
if row == n - 1:
solution = [row[:] for row in board]
solutions.append(solution)
board[row][col] = 0
col += 1
continue
row += 1
for solution in solutions:
NQueenProblem.print_board(solution)
print()
NQueenProblem.n_queen(4)
|
C#
using System;
using System.Collections.Generic;
class NQueenProblem
{
static void Print(int[,] board)
{
int count = 0;
foreach (int el in board)
{
if (el == 1)
{
count++;
}
}
if (count != board.GetLength(0))
{
return;
}
for (int i = 0; i < board.GetLength(0); i++)
{
for (int j = 0; j < board.GetLength(1); j++)
{
Console.Write(board[i, j] + " ");
}
Console.WriteLine();
}
}
static bool Validate(int[,] board, int i, int j)
{
int c;
for (c = 1; c <= j; c++)
{
if (board[i - 1, c - 1] == 1)
{
return false;
}
}
int r;
for (r = 1; r <= i; r++)
{
if (board[r - 1, j - 1] == 1)
{
return false;
}
}
c = j;
r = i;
while (c != 0 && r != 0)
{
if (board[r - 1, c - 1] == 1)
{
return false;
}
r--;
c--;
}
c = j;
r = i;
while (c != board.GetLength(1) + 1 && r != 0)
{
if (board[r - 1, c - 1] == 1)
{
return false;
}
r--;
c++;
}
return true;
}
static void NQueen(int n)
{
int[,] board = new int[n, n];
Stack<int[]> queensPositions = new Stack<int[]>();
int j = 1;
for (int i = 1; i <= board.GetLength(0); i++)
{
for (; j <= board.GetLength(1); j++)
{
if (Validate(board, i, j))
{
board[i - 1, j - 1] = 1;
queensPositions.Push(new int[] { i, j });
break;
}
}
j = 1;
if (queensPositions.Count != i)
{
if (queensPositions.Count > 0)
{
int[] qLast = queensPositions.Pop();
board[qLast[0] - 1, qLast[1] - 1] = 0;
i = qLast[0] - 1;
j = qLast[1] + 1;
}
}
if (i == board.GetLength(0))
{
Print(board);
Console.WriteLine();
if (queensPositions.Count > 0)
{
int[] qLast = queensPositions.Pop();
board[qLast[0] - 1,qLast[1] - 1] = 0;
i = qLast[0] - 1;
j = qLast[1]+ 1;
}
}
}
}
public static void Main(String[] args) { NQueen(4); }
}
|
Javascript
function print(board) {
let count = 0;
for (let i = 0; i < board.length; i++) {
for (let j = 0; j < board[i].length; j++) {
if (board[i][j] === 1) count++;
}
}
if (count !== board.length) return;
for (let i = 0; i < board.length; i++) {
let row = '';
for (let j = 0; j < board[i].length; j++) {
row += board[i][j] + ' ';
}
console.log(row);
}
}
function validate(board, i, j) {
for (let c = 1; c <= j; c++) {
if (board[i - 1] === 1) return false;
}
for (let r = 1; r <= i; r++) {
if (board[r - 1][j - 1] === 1) return false;
}
let c = j;
let r = i;
while (c !== 0 && r !== 0) {
if (board[r - 1] === 1) return false;
r--;
c--;
}
c = j;
r = i;
while (c !== board.length + 1 && r !== 0) {
if (board[r - 1] === 1) return false;
r--;
c++;
}
return true;
}
function n_queen(n) {
let board = Array(n).fill().map(() => Array(n).fill(0));
let queens_positions = [];
let j = 1;
for (let i = 1; i <= board.length; i++) {
for (; j <= board.length; j++) {
if (validate(board, i, j)) {
board[i - 1][j - 1] = 1;
queens_positions.push([i, j]);
break;
}
}
j = 1;
if (queens_positions.length !== i) {
if (queens_positions.length > 0) {
let Q_last = queens_positions[queens_positions.length - 1];
queens_positions.pop();
board[Q_last[0] - 1][Q_last[1] - 1] = 0;
i = Q_last[0] - 1;
j = Q_last[1] + 1;
}
}
if (i === board.length) {
print(board);
console.log('');
if (queens_positions.length > 0) {
let Q_last = queens_positions[queens_positions.length - 1];
queens_positions.pop();
board[Q_last[0] - 1][Q_last[1] - 1] = 0;
i = Q_last[0] - 1;
j = Q_last[1] + 1;
}
}
}
}
const n = 4;
n_queen(n);
|
Output
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
Time Complexity: O(n2 * n!), where n is the size of the board.
Space Complexity: O(n2)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...